Приближение Борна-Оппенгеймера

Сегодня мы поговорим о том, как квантовая механика практически уничтожила химию как науку, а Оппенгеймер, destroyer of worlds, стал её спасителем. Я понимаю, что читатель может не разделять моего пиетета по отношению к химии и поэтому может задаваться вопросом: а зачем мне читать эту статью? Я предлагаю такой ответ: на сегодняшнем примере вы увидите почему иногда стоит прыгать выше своей головы и не бояться познакомиться с теми островками знаний, которые изначально не вызывают ничего, кроме страха. В качестве бонуса немного поговорим о том, какие есть перспективные направления в химии (особенно будет полезно для тех, кто думает, что «быть химиком» это только про фармацевтику, заводы или преподавание в универе).

Мета-введение

Стоит обговорить на берегу, что в этой статье будут страшные формулы и уравнения. И это вполне осознанное решение: я вполне могу поверить в верность цитаты, приведенной Хокингом: «каждое уравнение в книге уменьшает ее продажи вдвое». Наверное поэтому львиная доля научпопа мне казалась поверхностной и всегда хотелось чуть больше строгости и точности. Давайте мы отложим дискуссию об оправданности включения формул на заключение, а пока я вам в двух словах расскажу о чем будет эта статья.

1. Сначала мы проведем некоторый анализ того, что мы уже знаем о химии и заметим, что фундаментальные вопросы, которые изучает химия, можно сформулировать в виде математической задачи.
2. Я скажу, что лучше всего с решением этой задачи справляется квантовая механика и покажу пример триумфальной точности квантмеха.
3. Мы познакомимся с двумя важнейшими инструментами квантовой механики: неким всеобъемлющим источником информации (волновой функций) и магической палочкой (оператор), которая позволит получать информацию из волновой функции.
4. Мы посмотрим куда приводит квантовая механика в своей строгой форме, а потом окажется, что нам придется сделать ряд очень смелых допущений, чтобы химия могла существовать как наука.
5. Мы познакомимся с ситуациями, в которых эти самые допущения не работают.
6. Подведем итоги и попытаемся понять что все это значит.

Все формулы и уравнения, которые будут в статье, будут играть роль некого математического «подтверждения» идей выше. Нет ничего страшного в том, что вы не будете «понимать» эти формулы; для нас гораздо важнее будет не сама форма каждого отдельно взятого уравнения, а то что мы с ней делаем (какие приближения). И во всех случаях, я постараюсь четко проговаривать, что важно, а что нет.

Особенно важен этот посыл школьникам: возможно вы привыкли, что к моменту изучения новой темы вы уже знакомы со всеми необходимыми пререквизитами^[1], и вы подумаете «ну мне сначала надо почитать больше про линейную алгебру или квантовую механику прежде, чем я смогу прочитать эту статью». Это глубоко ошибочная позиция, во взрослой жизни вы никогда не будете 100% готовыми, вы никогда не сможете выполнить все пререквизиты. Сейчас надо просто набраться смелости и посмотреть куда это вас приведет. Ну, а теперь, погнали!

Часть I. Фундаментальные вопросы химии

Что такое химия?

Какие мысли приходят вам в голову, когда вы слышите слово «химия»? Возможно вы думаете о химических превращениях (сгорание древесины, выпадение осадка при смешении двух растворов), а возможно о химических формулах (те самые загадочные \(\text{H}_2\text{O}\) или \(\text{C}_6\text{H}_6\)). Давайте остановимся на последних. Думаю вы встречались со структурными формулами молекул (а если вам повезло и вы успели дойти до изучения органической химии, то вы возможно рисовали их сами). Например, вот такими:

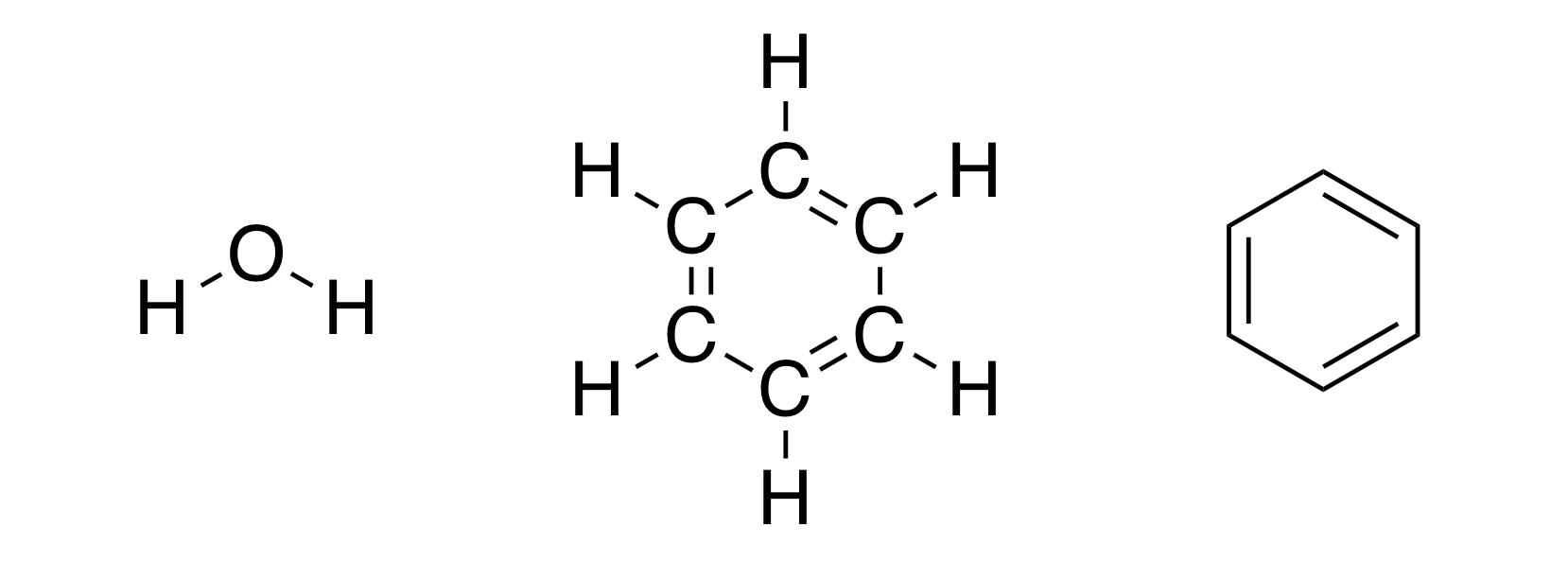
Забавно, что мы порой даже не задумываемся сколько информации (в виде неявных допущений) может быть скрыто в одной картинке. С одной стороны, выше просто нарисованы структурные формулы воды и бензола. Но если задуматься, то изображая эти молекулы именно так, мы учитываем, что обе связи кислород-водород в молекуле воды имеют одинаковую и определенную длину, что между связями должны быть определенные углы. Иначе как объяснить, что мы рисуем именно структуры выше, а не, например, ниже:

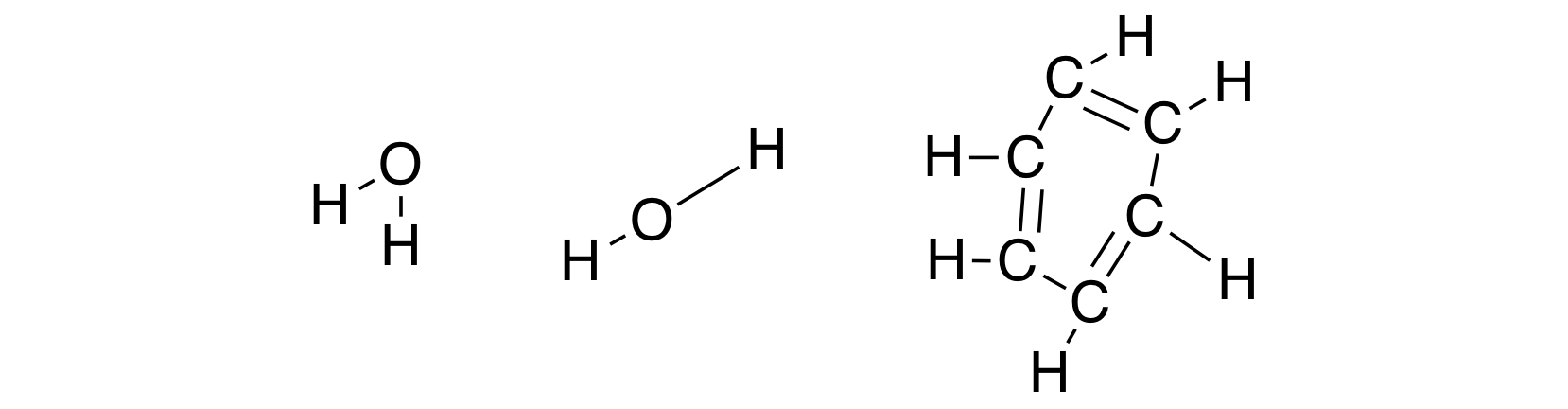
Но что определяет длины связей и угол между ними? Школьная химия предлагает следующую аргументацию: химические связи образуются когда два атома отдают электроны в общее пользование. Соответственно между электронами одного атома и ядрами другого атома происходит кулоновское притяжение. При этом, между электронами и между ядрами действует кулоновское отталкивание. Баланс этих двух сил и определяет равновесное расстояние и углы. Мы можем изобразить зависимость (потенциальной) энергии (мы ее будем обозначать как \(V\)) от межатомного расстояния \(R\) для двухатомных молекул (возможно вы уже встречались с таким графиком).

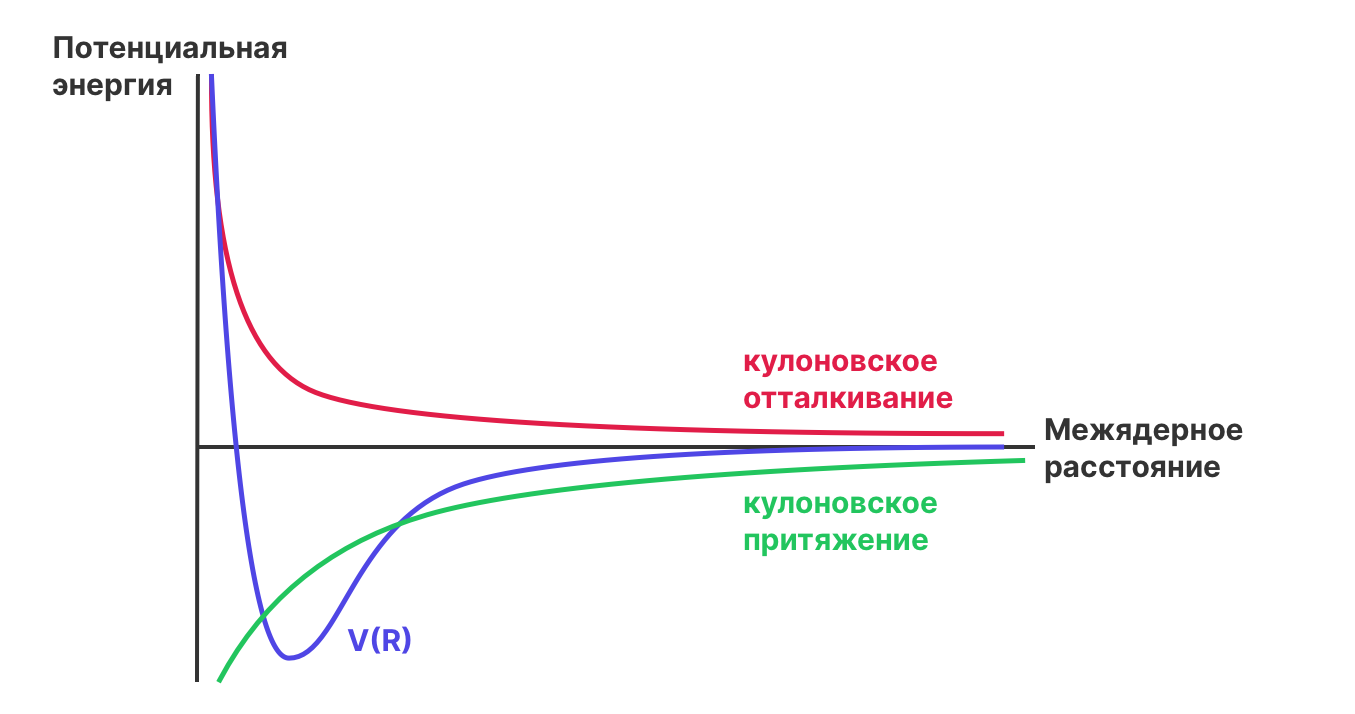
Если не ограничиваться двухатомными молекулами, мы получим зависимость потенциальной энергии \(V\) от всех независимых параметров, характеризующих структуру молекулы. Например, если принять за данность, что в молекуле воды обе связи \(\text{O-H}\) имеют одинаковую длину, то для однозначного описания структуры молекулы воды нужно уточнить длину этой связи \(R\) и угол между двумя связями (пусть будет \(\theta\)). В итоге, получаем зависимость \(V(R, \theta)\), изображенную на графике ниже. Вот эту поверхность мы называем поверхностью потенциальной энергии (PES, от английского Potential Energy Surface). Такие же поверхности (в многомерном пространстве их называют гиперповерхностями) существуют и для многоатомных молекул, но с ростом количества структурных параметров визуализация становится затруднительной.

Перейдите по ссылке, чтобы открыть интерактивную версию графика

Те допущения, которые мы делаем в процессе изображения молекул, можно сформулировать как утверждения, описывающие эту поверхность. Например, у этой поверхности должен быть минимум - точка, в которой потенциальная энергия минимальна^[2]. Именно расположение этой точки и определяет структуру нашей молекулы. Таким образом, поиск оптимальной структуры молекулы сводится к поиску минимума определенной функции.

Электронные орбитали

А теперь немного поговорим о химии, как о науке о превращениях. Химическая реакция сопровождается процессом разрушения и создания химических связей. А что образует связи? Электроны. А где находятся электроны? В орбиталях. В рамках школьной программы, вы скорее всего остановитесь на картинках атомных орбиталей:

На картинке выше слева направо, сверху вниз показаны формы \(1s, 2s, 2p, 3s, 3p, 4d\) орбиталей атома водорода. Кстати, эта оговорка про «атома водорода» совершенно не случайна. В это сложно поверить, но мы знаем точную форму атомных орбиталей (АО) только для атома водорода. Мы лишь предполагаем, что формы АО других элементов похожи на АО водорода. Можно задаться вопросом, а где находятся электроны в молекулах? Я думаю, что не сильно шокирую вас если отвечу: в молекулярных орбиталях (МО). Молекулярные орбитали выглядят таким образом:

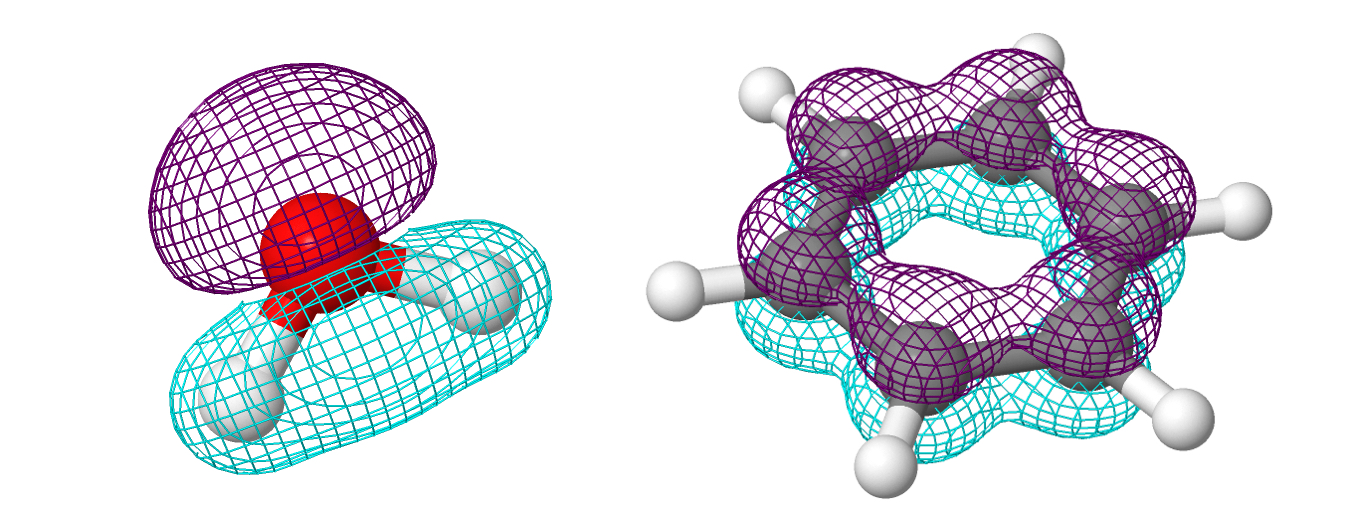
Для просмотра интерактивных графиков молекулярных орбиталей, пройдите по ссылкам: несколько орбиталей \(\sigma\)-системы и орбитали \(\pi\)-системы

Вы можете задаться вопросом, а как можно узнать форму МО? Этот вопрос сложнее, чем может показаться на первый взгляд. Нет ни единой причины почему МО должны быть похожи на АО, но нам кажется оправданным предполагать, что они все таки должны быть похожими. Поэтому основным методом поиска формы МО является т.н. теория линейной комбинации АО. Проще говоря, МО образуются в результате сложения и вычитания орбиталей с (потенциально) разными коэффициентами. Результат можно представить в виде диаграмм МО:

Таким образом, процесс поиска формы молекулярных орбиталей сводится к поиску коэффициентов, на которые надо помножить АО прежде, чем их сложить и получить МО.

Формализуем фундаментальные вопросы химии

Можем сформулировать идеи, описанные в двух секциях выше, в виде двух фундаментальных задач химии:

1. Поиск оптимальной структуры молекулы при знании формы PES. Иными словами, мы знаем, как электроны притягиваются к ядрам и отталкиваются от других электронов, и наша задача найти такую трехмерную форму молекулы, которая минимизирует отталкивания, и максимизирует притягивания.
2. Поиск оптимальных молекулярных орбиталей для определенной формы молекулы. Вся процедура поиска МО, описанная выше, велась для одной, фиксированной, геометрии молекулы. Если изменить любую из длин связей или любой из углов, МО станут другими.

Но подождите. Ведь форма поверхности потенциальной энергии зависит от взаимодействий электронов с ядрами и другими электронами. Эти взаимодействия зависят от того, где находятся электроны. Но расположение электронов (их орбитали) зависит от того, как расположены ядра. Получаем замкнутый круг. Что же делать? Пока можем только констатировать, что задачи, описанные выше, не являются независимыми друг от друга и не могут решаться по отдельности.

Часть II. Предсказательная способность квантовой механики

Самый точный способ описать структуру атомов (а вместе с ними и молекул) предлагает квантовая механика. Но прежде, чем мы перейдем к использованию инструментов этой теории, полезно понять почему научное сообщество принимает (а может даже и «верит» в) квантовую механику. Всё-таки идеи корпускулярно-волнового дуализма и замена электронных орбит и точного расположения электронов на распределения вероятности нахождения электронов в определенных точках пространства могут звучать (мягко говоря) нереалистично.

Точность квантовой механики

Физическая модель верна тогда, когда находится в согласовании с экспериментом (а еще лучше - может предсказывать его результаты). Экспериментальное значение энергии ионизации атома гелия \(5\;945\;204\;238(45)\) МГц (погрешность указана в скобках). Решение уравнения Шрёдингера предсказывает значение \(5\;945\;262\;288.62(4)\), но это не конечный ответ, а лишь стартовая точка. Если учитывать ненулевой размер ядер, релятивистские эффекты (зависимость массы от скорости), спин-орбитальные взаимодействия и поляризацию вакуума (в дело вступает квантовая электродинамика), имеем:

$$
\text{Теория: } 5\; 945\; 204\; 223(42) \\ \tag{1-2}
\text{Эксперимент: } 5\; 945\; 204\; 238(45)
$$

Как видим, квантовая теория предсказывает значение энергии с, без преувеличения, триумфальной точностью. И еще поразительнее, что результат теоретических расчетов ограничен точностью, с которой мы знаем массу атому гелия (она определяется экспериментальным путем). А знаем мы ее всего-лишь с 12 (двенадцатью) значащими цифрами. Theory will only take you so far, но такому so far можно только позавидовать. Теоретическое предсказание энергии ионизации взято из статьи 2001 года Владимира Коробова и Александра Елховского.

Часть III. Уравнение Шрёдингера

Одно из главнейших уравнений могучей квантовой теории можно записать четырьмя символами: \(\mathcal{\hat{H}} \Psi = E \times \Psi\). Понимать это стоит так:

• существует некий (математический) объект, который содержит в себе всю информацию о системе (атоме, молекуле). Это и есть волновая функция \(\Psi\).
• все физические характеристики, которые нас интересуют (в т.ч. энергия \(E\)), можно получить подвергая этот самый источник информации определенным преобразованиям, через воздействие операторов (например оператора Гамильтониана \(\hat{H}\) если нас интересует энергия).

Именно поэтому в уравнении нельзя «сократить» \(\Psi\): между \(\hat{H}\) и \(\Psi\) нет знака умножения, подразумевается воздействие \(\hat{H}\) на \(\Psi\).

Остановимся на каждом ингредиенте по отдельности.

Источник информации (волновая функция)

Как мы определили выше, волновая функция - это такой, практически, магический объект, содержащий информацию о системе. Если мы говорим о молекуле, то наверняка этот объект должен зависеть от расположения всех электронов (\(\mathbf{r}\)) и ядер (\(\mathbf{R}\)). Т.е. наш магический объект, это функция \(\Psi(\mathbf{r}, \mathbf{R})\).

Эту волновую функцию, зависящую от расположения электронов и ядер, можно разложить^[3] на бесконечную сумму произведения двух функций, каждая из которых по отдельности описывает либо электроны, либо ядра:

$$
\begin{aligned}
\Psi(\mathbf{r}, \mathbf{R}) = \sum_{k=0}^{N=\infty} \sum_{l=0}^{N=\infty} c_{kl} g_k(\mathbf{r}) h_l (\mathbf{R}) = \sum_k^{N=\infty} g_k(\mathbf{r}) \left[\sum_{l=0}^{N=\infty} c_{kl} h_l (\mathbf{R})\right] \\= \sum_k^{N=\infty} g_k(\mathbf{r}) f_k(\mathbf{R})
\end{aligned} \tag{3}
$$

Где мы переопределили функцию \(f_k(\mathbf{R})\) через сумму функций \(h_l(\mathbf{R})\), просто чтобы иметь суммирование не по двум координатам, а всего по одной. Понять это уравнение можно через интересную аналогию: \(g_k(\mathbf{r})\) и \(h_l (\mathbf{R})\) это своего рода простейшие элементы, из которых с помощью сложения (с определенными коэффициентами) мы получаем волновую функцию всей системы. Если рассматривать \(\Psi\) за некую «молекулу», то функции \(g_k(\mathbf{r})\) и \(h_l (\mathbf{R})\) это составляющие «атомы» (математики назовут их «базисными функциями»), а коэффициенты \(c_{kl}\) показывают важность этих «атомов». Дальнейшие преобразования делаются исключительно ради практической пользы.

Помните в первой части мы говорили, что точную форму АО мы знаем только для атома водорода? На самом деле, мы можем использовать АО водорода для описания любых молекул ровно потому, что волновые функции (на самом деле не только волновые) можно раскладывать на сумму базисных функций, а набор АО водорода формирует полноценный базис пространства функций. Иными словами, любую функцию можно представить суммой (с коэффициентами) функций АО водорода.

Разложение выше точно когда \(N=\infty\), но не сложно догадаться что работать с бесконечным набором функций... немного сложно. Оказывается, что можно немного упростить жизнь, если добавить в \(g_k\) параметрическую зависимость от \(\mathbf{R}\). Что такое параметрическая зависимость? Это значит, что в зависимости от \(\mathbf{R}\) меняется сама форма функции. Для такого расположения ядер, у нас есть такая функция расположения электронов. А если ядра передвинутся сюда, функция станет другой. В итоге получим:

$$
\Psi(\mathbf{r}, \mathbf{R}) = \sum_{k=0}^{N} \psi_k(\mathbf{r}; R) f_k(\mathbf{R}) \tag{4}
$$

где параметрическую зависимость мы обозначили после точки с запятой. Это разложение по-прежнему точно только в пределе \(N\to\infty\), но благодаря наличию вот этой самой параметрической зависимости если мы возьмем конечное количество \(N\) наша точность будет чуть выше чем раньше. Функция \(\psi_k(\mathbf{r}; R)\) - это электронная волновая функция, описывает, не угадаете, электроны. Функция \(f_k(\mathbf{R})\) описывает вращательно-колебательные движения ядер.

Весь текст выше - попытка объяснить откуда берется вот такое разложение (4). Для целей дальнейшего повествования важно не столько то, как мы пришли к этому разложению, а что мы будем дальше делать.

Преобразования, позволяющие узнать энергию

На уроках школьной физики мы узнаем, что энергия системы может находиться в двух формах: в виде потенциальной и кинетической энергии. Точно так же в квантовой механике есть преобразования (операторы), которые позволяют узнать кинетическую энергию, и отдельно есть операторы, которые позволяют узнать потенциальную энергию.

Давайте попробуем перечислить в общем случае от чего зависит энергия двухатомной молекулы:

• кинетическая энергия первого ядра (\(a\))
• кинетическая энеpгия второго ядра (\(b\))
• кинетическая энергия электронов (обозначим каждый за \(i\), всего их \(n\))
• кулоновское отталкивание ядер
• кулоновское притяжение электронов к первому ядру
• кулоновское притяжение электронов ко второму ядру
• кулоновское отталкивание электронов

Общая энергия должна быть суммой этих составляющих. Остается лишь записать эти энергии на языке квантовой механики:

$$
\begin{aligned}
\mathcal{\hat{H}} &= -\frac{\hbar^2}{2M_a} \Delta_a -\frac{\hbar^2}{2M_b} \Delta_b - \sum_{i=1}^n \frac{\hbar^2}{2m} \Delta_i + V \\
V &= \frac{\mathcal{Z}_a \mathcal{Z}_b e^2}{R} - \mathcal{Z}_a \sum_i \frac{e^2}{r_{ai}} - \mathcal{Z}_b \sum_i \frac{e^2}{r_{bi}} + \sum_{i<j} \frac{e^2}{r_{ij}}
\end{aligned} \tag{5-6}
$$

где \(\mathcal{Z}_a\) и \(\mathcal{Z}_b\) - заряды ядер, \(M_a\) и \(M_b\) - массы ядер, \(e\) - элементарный заряд, \(R\) - межатомное расстояние, и \(r_{ai}\) и \(r_{bi}\) - расстояния от электронов до первого и второго ядра. Слагаемые строке (5) перечисляют кинетические энергии двух ядер и всех электронов. Слагаемые на строке (6) перечисляют потенциальные энергии кулоновских взаимодействий. Полная форма оператора Гамильтониана может вас пугать, но я повторю -- это не больше, чем результат перевода списка взаимодействий с русского языка на язык математического аппарата квантовой механики, а значит, если вы захотите, вам достаточно будет изучить этот словарь, чтобы самому воссоздавать такие записи.

Стоит немного остановиться на загадочных треугольниках \(\Delta_i\) - это математический оператор, который подразумевает поиск скорости изменения функции в пространстве. Возможно вы уже задаетесь вопросом: а изменение относительно чего? В форме, записанной выше, подразумевается наличие привычной (абсолютной) системы координат \((x,y,z)\). Оказывается, что полезно разделять движение системы (например, молекулы) на движение ее центра масс (что определяет положение молекулы целиком) и относительные движения компонентов внутри (например, электронов относительно ядер). Чтобы сменить систему координат достаточно провести ряд алгебраических преобразований, и конечный результат будет таким:

$$
\begin{aligned}
\mathcal{H} &= \left[ -\frac{\hbar^2}{2M}\Delta_{XYZ} \right] + \hat{H}_0 + \hat{H}' \\
\hat{H}_0 &= -\sum_i \frac{\hbar^2}{2m}\Delta_i + V \\
\hat{H}' &= -\frac{\hbar^2}{2\mu}\Delta_\mathbf{R} + \hat{H}'' \\
\hat{H}'' &= - \frac{\hbar^2}{8\mu} \left(\sum_i\nabla_i\right)^2 + \frac{\hbar^2}{2}\left(\frac{1}{M_a} - \frac{1}{M_b} \right) \nabla_\mathbf{R} \sum_i \nabla_i \\
\end{aligned} \tag{7-10}
$$

Стало страшнее, но разобраться все еще можно. Первое слагаемое в уравнении (7) это кинетическая энергия от движения центра массы. Остальные слагаемые сгруппированы в два слагаемых \(\hat{H}_0\) и \(\hat{H}'\). Первое обычно называют электронным Гамильтонианом, т.к. оно содержит кинетическую энергию электронов (та самая \(\Delta_i\)). \(V\) такое же, как определено в уравнении (5), т.е. оно содержит все возможные формы потенциальных энергий. \(\hat{H}'\) содержит кинетическую энергию от относительного движения ядер (\(\Delta_\mathbf{R}\), где \(\mathbf{R}\) - это расстояние между ядрами \(a\) и \(b\)) и слагаемое \(\hat{H}''\) которое отвечает за корреляцию движений ядер и электронов (\(\nabla_i\) - другой оператор, показывает скорость движения). Разделение слагаемых на \(\hat{H}_0\), \(\hat{H}'\) и \(\hat{H}''\) может казаться необоснованным, тем не менее является полезным. Про первое слагаемое в уравнении (7) мы забудем и возвращаться к нему не будем (нас все таки интересует внутреннее устройство атомов и молекул, а не то как они перемещаются в пространстве).

Часть IV. Собираем все воедино

Итак, давайте попробуем собрать оба ингредиента: источник информации (волновую функцию) и операцию (оператор Гамильтониана) позволяющую достать информацию об энергии. Наша волновая функция:

$$
\begin{aligned}
\Psi(\mathbf{r}, \mathbf{R}) = \sum_{k=0}^{N} \psi_k(\mathbf{r}; R) f_k(\mathbf{R})
\end{aligned} \tag{11}
$$

И наш оператор:

$$
\begin{aligned}
\hat{H} = \hat{H}_0 -\frac{\hbar^2}{2\mu}\Delta_\mathbf{R} + \hat{H}''
\end{aligned} \tag{12}
$$

где, напомню, \(\hat{H}_0\) содержит информацию о кинетической энергии электронов и кулоновских взаимодействиях между электронами и ядрами, второе слагаемое с «лежачим» треугольником - это кинетическая энергия ядер^[4], а \(\hat{H}''\) содержит информацию о корреляции движения ядер и электронов.

И для полноты картины, давайте вспомним для решения каких задач мы вообще полезли в квантовую механику:

1. Поиск оптимальных структурных параметров (т.е. значений \(\mathbf{R}\)): какая геометрия молекулы наиболее стабильна?
2. Где находятся электроны (т.е. значения \(\mathbf{r}\)) в наиболее стабильной форме молекулы?

И это при всем при том, что стабильность геометрии молекулы зависит от того, где находятся электроны, а поэтому полностью разделить первую задачу от второй невозможно.

Внутри математического формализма выше, задача сводится к определению базиса (т.е. \(g_k(r)\) и \(h_l(R)\)) и поиску коэффициентов \(c_{kl}\). Ну или поиску формы функций \(\psi_k(\mathbf{r}; R) f_k(\mathbf{R})\) для как можно большего количества значений \(k\) (в идеале - бесконечного). Вы, возможно задаетесь, как можно найти форму функции, и действительно, задача крайне сложная. Математически она требует решения следующего уравнения (и это только для \(f_k(\mathbf{R})\)):

$$
\begin{aligned}
\left[ -\frac{\hbar^2}{2\mu}\Delta_{\mathbf{R}} + E_k^0(\mathbf{R}) + H_{kk}''(\mathbf{R}) - E \right]f_k(\mathbf{R}) = -\sum_{l(\neq k)}^N \Theta_{kl}f_l(\mathbf{R})
\end{aligned} \tag{13}
$$

где \(E_k^0\) это энергия, полученная благодаря \(\hat{H}^0\), \(E\) - общая энергия молекулы, а \(\Theta_{kl}\) это показатель связанности/сцепленности^[5] разных энергетических уровней \(k\) и \(l\). Чтобы уравнение казалось еще страшнее, я скажу, что часть операторов подразумевает дифференциирование, т.е. перед вами система взаимосвязанных дифференциальных уравнений.

$$
\begin{aligned}
\Theta_{kl} = -\frac{\hbar^2}{\mu} \langle \psi_k \vert \nabla_{\mathbf{R}} \psi_l \rangle_{e} \nabla_{\mathbf{R}} + H''_{kl}
\end{aligned} \tag{14}
$$

С помощью этих уравнений можно найти \(f(\mathbf{R})\), но для этого нужны \(\psi_k\), которые нужно как-то выбрать. Мы, практически, встали в тупик, и дальше делать нам нечего. Поэтому на сегодня все, всем спасибо, структура молекул непознаваема. До новых встреч!

Приближение Борна-Оппенгеймера

Если слагаемые \(\psi_k\) в разложении (11) достаточно сильно отличаются друг от друга (что, как правило, подразумевает различие на энергетической шкале), то их сцепленностью можно пренебречь^[6], и тогда \(\Theta_{kl}=0\) для всех \(k\neq l\). В таком случае, система уравнений сильно упрощается, ибо получаем зависимость только от одной функции \(f_k\).

$$
\begin{aligned}
\left[ -\frac{\hbar^2}{2\mu}\Delta_{\mathbf{R}} + E_k^0(\mathbf{R}) + H_{kk}''(\mathbf{R}) \right]f_k = E f_k
\end{aligned} \tag{15}
$$

Идем дальше, и говорим, пусть тогда вся наша волновая функция будет описываться следующим произведением:

$$
\begin{aligned}
\Psi(\mathbf{r}, \mathbf{R}) \approx \psi_k(\mathbf{r}; R) f_k(\mathbf{R})
\end{aligned} \tag{16}
$$

Иными словами, мы оставляем только одно слагаемое из разложения, в котором изначально было бесконечное количество слагаемых. У такой формы есть очень приятная интуитивная интерпретация. Квадрат модуля волновой функции можно интерпретировать как плотность вероятности. Почему плотность? Потому что если взять квадрат модуля и умножить на определенный объем пространства, мы получим вероятность того, что в этом объеме будет частица. Так вот, в таком случае уравнение (16) говорит: если вы хотите знать вероятность того, что ядро находится в позиции \(\mathbf{R}\) а электроны в позиции \(\mathbf{r}\), то можно сначала взять вероятность того, что ядра находится в \(\mathbf{R}\), а потом помножить на условную вероятность, что электроны находятся в \(\mathbf{r}\) при том, что ядра находятся в \(\mathbf{R}\).

Это как вероятность того, что на улице идет дождь, а у вас в руках зонтик, является произведением вероятности того, что на улице идет дождь и условной вероятности того, что вы взяли зонтик, если на улице дождь.

Нам осталось сделать последний шаг: \(E_k^0(\mathbf{R})\) определяется кинетической энергией электронов (которая зависит от их массы, а точнее \(1/m\)) и потенциальной энергией, а все слагаемые внутри \(H_{kk}''(\mathbf{R})\) зависят от массы ядер (а точнее, зависимость \(1/M\) или \(1/\mu\)). Поскольку ядра атомов значительно (в 1836 раз^[7]) тяжелее электронов, \(H_{kk}''(\mathbf{R})\) будет иметь малые значения по сравнению с \(E_k^0(\mathbf{R})\), а поэтому мы можем им пренебречь и взять \(H_{kk}''(\mathbf{R})=0\)^[8].

В итоге получим следующее уравнение:

$$
\begin{aligned}
\left[ -\frac{\hbar^2}{2\mu}\Delta_{\mathbf{R}} + E_k^0(\mathbf{R}) \right]f_k(\mathbf{R}) = E f_k(\mathbf{R})
\end{aligned} \tag{17}
$$

Справа у нас энергия системы \(E\), а слева два слагаемых. Один содержит «лежачий» треугольник, значит, вы возможно догадаетесь, он связан с кинетической энергией. Общая энергия состоит из кинетической и потенциальной. Значит второе слагаемое - это потенциальная энергия. Возможно вы помните, что \(E_k^0(\mathbf{R})\) получилась из \(\hat{H}_k^0\), который содержал информацию об электронах. Потенциальная энергия связанная с расположением электронов?

Это же та самая поверхность потенциальной энергии или PES, о которой мы говорили в самом начале! Это та самая поверхность, которая определяет структуру молекулы! Здесь она определяет решение уравнения (17), т.е. функцию \(f_k(\mathbf{R})\), которая и содержит информацию о равновесной (оптимальной) геометрии нужной нам молекулы.

Важно заметить, что само понятие поверхности потенциальной энергии появилось только после того, как мы применили приближение Борна-Оппенгеймера, математическая суть которого, сводится к тому, что мы взяли бесконечную сумму (11) и оставили от нее только одно слагаемое (16). Не имея нужных познаний линейной алгебры, вы, скорее всего, приняли за данность шаги (3)-(4), но даже так, чисто на интуитивном уровне вам было легче поверить, что функцию можно представить как бесконечную сумму других функций, чем что можно просто взять и оставить только одно слагаемое в (16). Насколько оправдан такой шаг - вопрос отдельный, примечательно то, что без такого приближения не появится поверхность потенциальной энергии. Вместо нее будет бесконечная сумма таких поверхностей, каждая определяющая различные позиции ядер. А без единой поверхности потенциальной энергии нет единой структуры.

Сама концепция наличия определенной структуры молекулы появляется только после применения приближения Борна-Оппенгеймера.

В противном случае, все что мы имеем -- распределение вероятности различных структур. Так же как у электрона нет четкой орбиты, по которой он крутится вокруг ядра, а вместо этого есть лишь распределение вероятности найти электрон в той или иной точке, у ядер нет четкого положения, есть лишь распределение вероятности. А значит нет четких химических связей, нет четких длин этих связей или углов между ними. Все, что мы могли бы сказать про структуру молекулы бензола \(\text{C}_6\text{H}_6\), это то, что у молекулы есть сферическая симметрия, а расположения электронов и ядер взаимосвязаны.

Примерно то же самое, мы бы могли сказать и про структуру молекулы воды, и про молекулу белка. Мы бы могли посчитать среднее расстояние между двумя углеродами, но поскольку все атомы углерода неотличимы^[9], мы бы получили среднее значение расстояний между любыми двумя атомами углерода, а не только соседними. Понять, что молекула имеет форму плоского шестиугольника было бы, скорее всего, невозможно.

И на самом деле, учитывая то, что истинная волновая функция (11) это не одно слагаемое, а сумма, привычный плоский шестиугольник - не больше, чем одна из форм, принимаемой молекулой. Некоторые называют такую форму «Борн-Оппенгеймеровская структура», дабы подчеркнуть, что ее существование возможно только после применения соответствующего приближения. У молекулы бензола есть, как минимум, 217 разных структурных изомеров, т.е. Борн-Оппенгеймеровских структур (если учитывать стереоизомерию, цифра поднимается до 328)^[10]. Из них 17 ацикличных, 71 содержат один цикл, 134 два цикла, 87 три цикла и 19 четыре циклов. Это структуры, которые удовлетворяют требования валентности углерода и водорода; понятное дело, что многие из них нестабильны. Но из них аж 80 достаточно стабильны, чтобы их можно было синтезировать, и аж 40 разных вариаций Борн-Оппенгеймеровских \(\text{C}_6\text{H}_6\) были синтезированы на практике.

Осознаем последствия

Давайте еще раз проговорим: без приближения Борна-Оппенгеймера у молекул нет тех самых четко определенных структур, которые мы привыкли рисовать на уроках химии. Мы не можем быть уверенными, что молекула бензола выглядит именно так, какой мы ее рисуем. В таком случае, все разделы химии, которые работают со структурой молекул, просто теряют смысл. Та же органическая химия вся построена на том, что мы рисуем две разные структуры и пытаемся понять как можно поменять связи так, чтобы из реагента получить продукт. Химия, как наука, не могла бы сдвинуться с точки «есть молекулы, в которых есть ядра и электроны, движения ядер и электронов сильно взаимосвязаны». Иными словами, ее бы просто не существовало.

И здесь мы приходим к первому мета-выводу статьи. Иногда гораздо полезней пытаться описывать окружающий мир с помощью ошибочных^[11], но полезных моделей (какой является концепция 3D структур). Звучит, наверное, банально, но сколько из вас при изучении новой темы ставит себе задачу понять все на самом доскональном уровне, дойдя до фундаментальных основ? До них то дойти можно, но как мы видим, бывает так, что фундаментальная «истина» оказывается... непрагматичной?

И нам просто повезло, что в большинстве ситуаций слагаемое \(f_k(\mathbf{R})\) с наименьшей энергией имеет энергию значительно ниже, чем у других слагаемых и поэтому определяет структуру молекулы в большей степени. Но примечательно, что стабильность слагаемых в разложении (11) может меняться в зависимости от химического окружения. Например, сам по себе бензол предпочитает быть в виде плоского шестиугольника, но если добавить щепотку стерических отталкиваний, например заменив три водорода на терт-бутильные заместители, внезапно наиболее стабильной структурой уже будет бензол Дьюара.

Часть V. Конические пересечения

Когда мы переходили от (13) к (15), мы приняли, что разные слагаемые в разложении (11) отличаются достаточно, чтобы между ними практически не было сцепленности, т.е. мы посчитали возможным принять \(\Theta_{kl}=0\). Возможно еще тогда у вас возник вопрос: а что если разные слагаемые все таки сцеплены? Бывают ли случаи, когда мы не можем принять сцепленность равной нулю?

Бывают. Разные слагаемые в (11) мы называем диабатическими кривыми/состояниями. Каждым из них соответствует своя поверхность потенциальной энергии. Существуют такие точки конфигурационного пространства^[12], в которых две диабатические кривые находятся достаточно близко друг другу, и может даже пересекаются. Такие пересечения называются коническими.

Перейдите по ссылке, чтобы открыть интерактивную версию графика

Вблизи этих самых конических пересечений, как вы уже могли догадаться, \(\Theta_{kl}\neq 0\) и приближение Борна-Оппенгеймера теряет свою силу. И для корректного описания этих регионов энергетических гиперповерхностей нужно искать методы решения уравнения (13).

И возможно все это время вы думали, что все, о чем мы говорим - это крайне абстрактные и экзотические концепты, которые представляют интерес только для теоретических физиков. А нет, конические пересечения играют фундаментальную роль в понимании механизмов фотохимических реакций. Для тех, кто знаком с теорией переходных состояний в органической химии - конические пересечения в фотохимических реакциях это как переходные состояния в термических.

Фотостабильность белков

Возможно вы удивитесь почему в статье о квантовой механике внезапно появились основные игроки современной биологии. Все мы знаем, что наше Солнце, будучи термоядерным реактором, излучает довольно вредные УФ-лучи. Возможно вы знаете, что УФ-лучи способны ломать химические связи (иногда это полезно: так происходит биосинтез витамина Д3). И вот вам вопрос: а что мешает УФ-излучению ломать химические связи внутри молекул белка? УФ излучение без проблем может пройти через фосфолипидную мембрану, т.е. до белков оно точно доходит. И хоть вопрос крайне простой (на уровне «почему небо голубое»), ответ на него может дать только квантовая механика.

Фотостабильность белков (а значит и всех живых организмов) сводится к диабатическим состояниям водородной связи. Пусть в основном (изначальном) состоянии у нас есть некая связь \(\text{X}-\text{H}\) и атом \(\text{Y}\), имеющий неподеленную электронную пару. Между ними есть водородная связь \(\text{X}-\text{H}\cdots \text{Y}\). Обозначим это состояние как \(S_0\). Поглощение УФ-излучения переводит систему в первое возбужденное состояние \(^1LE\), недалеко от минимума которой расположено коническое пересечение с другим состоянием \(^1 CT\). Этому состоянию соответствует другое слагаемое в разложении (11), а значит другая функции \(\psi(\mathbf{r})\) и \(f(\mathbf{R})\). Новая функция \(\psi\) подразумевает несколько другое расположение электронов: один электрон переходит от связи \(\text{X}-\text{H}\) к атому \(\text{Y}\) образуя \((\text{X}-\text{H})^+ \cdots \text{Y}^-\), что называется charge-transfer complex (комплекс с переносом заряда), отсюда и название состояния CT. Новая функция \(f(\mathbf{R})\) имеет минимум в точке пространства, где атом водорода уже находится рядом с атомом \(\text{Y}\): т.е. \(\text{X}^- \cdots (\text{H}-\text{Y})^+\), На пути к минимуму этого состояния есть еще одно коническое пересечение, в этот раз с изначальным состоянием \(S_0\). Но в этом состоянии минимуму уже соответствует позиция водорода ближе к атому \(\text{X}\) и процесс релаксации сопровождается возвращением в изначальное состояние. Энергия, которая освобождается в результате движения по диабатическим кривым в направлении более стабильных состояний рассеивается в виде тепла, меняя колебательные состояния окружающих молекул. Простыми словами, энергия УФ-фотона не вредит химическим связям и всего-лишь нагревает воду внутри клеток.

Примечательно, что процесс был описан в 2006 году. Т.е. то, что мы обсуждаем находится на рубежах человеческих познаний. Если для вас это недостаточно свежо, вот примечательный факт. У волновых функций есть т.н. фаза^[13]. В процессе перехода через коническое состояние фаза волновой функции изменяется. 28 августа 2023 года в Nature Chemistry вышла статья, описывающая экспериментальное наблюдение конического пересечения на квантовом компьютере. Четыре. Недели. Назад.

Конические пересечения и ДНК

На уроках биологии вы узнаете, что один из строительных блоков ДНК - аденин (систематическое название которого 6-аминопурин). А вы когда-нибудь задумывались почему аденин имеет именно такую структуру? У биологии есть козырный ответ: «это наиболее выгодно с точки зрения эволюции». Ну хорошо, пусть эволюция выбрала аминопурины. А задавались ли вы вопросом: а почему именно 6-аминопурин, а не, скажем, 2-аминопурин?^[14] Главный и практически единственный критерий, который мы предъявляем к нуклеотидным основаниям на уроках биологии - способность организовывать водородные связи. 2-аминопурин может связываться с тимином так же хорошо, как и 6-аминопурин.

Научное сообщество предполагает^[15], что 6-аминопурин был выбран благодаря большей фотостабильности: 6-аминопурин находится в возбужденном состоянии (после поглощения УФ излучения) всего 1 пикосекунду (это \(10^{-15}\) секунд), тогда как 2-аминопурин может находиться десятые доли наносекунды (это \(10^{-10}\) секунд). Т.е. 6-аминопурин стабильнее на 5 порядков или в 100 000 раз. Почему нам важно как долго молекула находится в возбужденном состоянии? Потому что в этом возбужденном состоянии молекула может вступать в фотохимические реакции, например димеризации, приводя к повреждению ДНК (такие повреждения коллективно называют DNA lesions). Почему 6-аминопурин способен возвращаться в основное состояние настолько быстрее? Потому что у него есть доступ к коническому пересечению. Т.е. коническое пересечение не просто позволяет объяснить фотостабильность ДНК, оно еще и оказывается причиной^[16] почему были выбраны именно такие нуклеотиды.

Этот механизм не гарантирует полную защиту от УФ излучения. DNA lesions все равно образуются в результате воздействия УФ лучей. Когда мы говорим, о фотостабильности ДНК или белков, мы говорим о том, что они получают непоправимый вред сильно реже, чем если бы вышеописанных механизмов не существовало. Если бы 6-аминопурин сидел в возбужденном состоянии в 100 000 раз дольше, страшно подумать во сколько раз больше формировалось бы нуклеотидных димеров. Возможно, что настолько много, что живые организмы просто не смогли бы существовать.

Часть VI. Делаем выводы

Пришла пора оглянуться и осмыслить что мы сегодня узнали:

1. Мы определили, что описание структуры атомов и молекул сводится к поиску формы гиперповерхности потенциальной энергии и поиску оптимальных молекулярных орбиталей для структуры, определенной минимумом той поверхности.
2. Мы узнали, что для описания структуры атомов и молекул нужно пользоваться инструментами квантовой механики. Например, волновой функцией \(\Psi\) и оператором \(\hat{H}\). Мы начали с того, что перечислили типы взаимодействий внутри молекул, а потом переписали их на языке математического аппарата квантовой механики (5)-(10).
3. Мы узнали, что волновые функции можно раскладывать на бесконечную сумму более простых функций (4). Мы записали конечное уравнение (13)-(14), позволяющее описывать структуру молекул.
4. Оказалось, что просто для того, чтобы у молекул была определенная трехмерная структура, нам нужно сделать ряд очень смелых допущений (приближение Борна-Оппенгеймера): взять лишь одно слагаемое из бесконечной суммы и принять равным нулю ряд взаимодействий.
5. Мы узнали, что благодаря тому, что существуют ситуации, в которых это приближение перестает работать, поглощение УФ излучения белками и ДНК приводит к нарушению структуры сильно реже, чем могло бы быть. Иными словами, благодаря коническим пересечениям наша жизнь становится возможной.

Я не знаю, что к этому моменту чувствует читатель, поэтому позволю себе провести небольшой анализ на основании того, что чувствую я (и чувствовал, когда впервые изучил эту тему). Очень сложно передать словами это ощущение одновременного страха и восхищения. Страха от того, как много ты не знаешь. Восхищения от того, что есть безграничные просторы, которые познаваемы. Столько вопросов, на которые ты не знаешь ответа и еще столько же, на которые эти ответы не найдены вовсе. И тут мы подходим к обсуждению причин почему в этой статье так много страшных формул.

Не знаю как было у вас, но я покидал стены школы с неким ощущением, что вроде бы я понимаю общие очертания научных дисциплин, и остается только выбрать одно направление, в котором ты будешь получать узкую специализацию. Не то, чтобы у меня была прям самоуверенность (хотя кто его знает, я сейчас говорю то, о том, каким я запомнил себя, а не каким я был на самом деле), правильнее, пожалуй, сказать, что у меня не было страха от того, что я практически не знаю ничего. Страх, который появился года три назад, когда я серьезно начал углубляться в квантовую механику. И лично мне, я считаю, было бы полезнее, если бы этот страх появился раньше. Речь, конечно же, не о самом страхе самом по себе, а о том, что он сопровождает: понимание неизученных просторов науки.

Нет школьника, который в 11-12 классе не задумывается о том, чем он будет заниматься по жизни. Но какие мысли приходят в его голову, когда он думает о химии? Реакции? Смешение пробирок? Фармацевтика? Нефтянка? Химия, там конечно есть, но давайте просто посмотрим сколько новых направлений мы затронули только в этой статье:

1. Можно пользоваться Борн-Оппенгеймеровской структурой молекулы, полученной в ходе решения уравнения (17) и изучать электронную структуру этой молекулы. Например, понимание энергетики электронных переходов позволяет создавать более эффективные квантовые точки, полупроводники лежащие в основе передовых экранов (QLED).
2. Можно заметить, что химическая реакция, это, по сути, не больше, чем движение по гиперповерхности потенциальной энергии системы, образованной из реагентов, из одной точки пространства в другую. Таким образом, изучение механизмов химических реакций сводится к изучению этой саомй гиперповерхности. На практике, можно искать переходные состояния интересующих реакций и оценивать их энергетику. Повторять расчеты для разных структур и таким образом определять какие молекулы стоит синтезировать, а какие нет.
3. А можно (и нужно) заниматься разработкой новых методов изучения этих самых гиперповерхностей. Что временами может сводиться к чистой математике. Например, в 2019 году был опубликован метод поиска минимальных энергетических путей (по которым и протекают химические реакции) через поиск геодезических кривых в Римановых многообразиях. Иными словами, применение инструментов дифференциальной геометрии позволило делать за 5 минут то, на что раньше уходило несколько дней.
4. Можно применять инструменты квантовой механики для изучения биологии. Если вас заинтересовал механизм, описывающий фотостабильность белков, можно начать изучать другие примеры proton coupled electron transfers (PCET). А можно открыть ящик пандоры вторичных сил, влияющих на структуру белка. Например, оказывается, что в некоторых белках есть \(n\to\pi^*\) взаимодействия, сила которых сравнима с силой водородных связей. \(n\to\pi^*\) взаимодействия - прямое следствие формы молекулярных орбиталей, которые получаются с помощью решения уравнения Шрёдингера.

Когда (да, надеюсь, что именно когда, а не если) вы начнете углубляться в любое из направлений описанных выше, вы внезапно столкнетесь с тем, что будете читать вроде бы текст на английском, а вроде бы и на инопланетном. Будет много формул и терминологии, которая вам до этого никогда не попадалась. Примерно как в этой статье, а скорее всего и хуже. В таких ситуациях у вас всегда есть выбор:

1. Я не понимаю 30/50/70/90% (нужное подчеркнуть) того, о чем тут говорится, поэтому я сделаю вывод, что это не для меня (или мне не по силам) и я перестану это читать.
2. Я не понимаю 30/50/70/90% (нужное подчеркнуть) того, о чем тут говорится, поэтому давай сначала я просто приму эти слова/формулы за некий абстрактный объект и попытаюсь понять какую идею/взаимосвязь между ними пытается выстроить этот текст. После одного-двух-трех прочтений, я скорее всего пойму какие из этих объектов первостепенны, а какие приведены для полноты картины. Потом если надо, я пойду и попробую изучить эти объекты более детально.

Эта проблема не встает так остро в школе, потому что как правило школьная программа выстроена так, что к моменту изучения новой темы, ученики уже знают (или хотя бы изучали) все необходимые пререквизиты. Лично я не могу вспомнить когда в последний раз я был в подобной ситуации: что я начинаю изучать новую тему и понимал, что все необходимые инструменты (пререквизиты) для ее понимания я уже знаю. Наверное такое возможно только в школе. Или правильнее сказать, при изучении науки, такое возможно только в школе.

И тогда, возможно, опция, которую вы выбираете из двух вышеперечисленных, может играть роль небольшого теста - насколько вы готовы связать свою жизнь с наукой. И мне кажется, что этого выбора достаточно: не важно сколько (и что) вы знаете и умеете сейчас, если вы готовы пробираться через неизвестные ранее термины и формулы, то у вас есть все, что нужно, чтобы добиться определенных успехов. И применимо это не только к квантовой механике, если заменить термины и формулы на молекулы и реакции, названия белков и регуляторные цепочки, алгоритмы и структуры данных, то я уверен тоже самое можно сказать и про экспериментальную химию, и про биологию, и про программирование.

И если вы дочитали до этих строк, то скорее всего вы уже знаете какой выбор вы готовы и хотите делать. А значит вам остается лишь продолжать развиваться и постигать новые горизонты. Все в ваших руках.

Эпилог

На написание первоначальной версии статьи ушло 12 часов. 6.13 часов ушло на создание иллюстраций. Еще 5.13 часа ушло на редактуру. И наконец 1.33 часа на подготовку публикации. Естественно все это время прошло под саундтрек Людвига Йоранссона. Отдельная благодарность Адылхан Арай, Загрибельному Богдану, Кайроллаеву Ернуру, Бисенали Санжару, и Тырину Андрею за полезные комментарии к первому черновику статьи.