[Прелесть физики] Метрология и Международная система единиц СИ. Часть II
![[Прелесть физики] Метрология и Международная система единиц СИ. Часть II](/content/images/size/w2000/2020/12/thermometer.jpg)
Все статьи из цикла "В чем прелесть предмета"
Другие статьи из цикла "В чем прелесть физики":
"Я знаю, что ничего не знаю"
Метрология и Международная система единиц СИ. Часть I
Постигая Вселенную: опасности на пути к звездам
Большой адронный коллайдер – спасение современной физики
Зачем нам теория всего?
В прошлой статье Метрология и Международная система единиц СИ. Часть I мы окунулись в удивительный мир физических величин и единиц измерения, узнав, как люди научились измерять и почему так важны естественные постоянные. Зародившись во времена древних цивилизаций, метр и секунда проделали долгий и тернистый, но оттого и захватывающий путь от самодельного вещественного эталона до переопределения через природные константы. Остальные единицы измерения СИ ждал не менее запутанный путь – путь познания окружающего мира человеком. Сейчас же давайте познакомимся с долгожданными килограммом и Кельвином!
Килограмм
Масса – невероятно важная величина, описывающая фундаментальные свойства материи. Массой обладают все макроскопические тела, будь то одно яблоко, мешок муки, огромная гора или целая планета, а также большинство элементарных частиц – протоны, электроны, позитроны и другие. Хотя в античные времена слово «масса» означало кусок теста, а не физическое свойство объектов, ее глубинное понимание уже существовало в умах древних людей. Так, например, в V веке до нашей эры жители Месопотамии научились взвешивать различные тела. В то время весы уже использовались повсеместно как прибор измерения массы, пусть самой массы как величины ещё не существовало. А весами люди попросту сравнивали значения массы, при этом не зная, что это и в чём ее измерять.
В Средневековье появилась первая единица массы – «фунт». Но таких «фунтов» было огромное множество, хоть отбавляй: английский, русский, шведский, испанский, датский и многие другие. Все эти единицы были различны, а большинство из них составляло около \(0.4\)–\(0.6\) кг. Однако с принятием метра и привязке его к Парижскому меридиану в \(1795\) году французы приняли новую единицу массы «грав», определив ее как массу тающего льда объёмом в \(1\) куб с ребром в одну сотую метра (\(0.01\) м). Вскоре обнаружив, как неудачно «грав» созвучен с дворянским титулом «грав» и словом «могила» (grave), ученые наделили «грав» всем нам знакомым именем «грамм». Как оказалось на практике, грамм – слишком маленькая величина, поэтому вместо грамма в качестве стандарта массы было решено использовать килограмм, равный \(1000\) граммам. По этой же причине на сегодняшний день килограмм является единственной величиной в системе СИ, имеющей дольную приставку.
Вскоре история метра повторилась уже с килограммом. Французский химик Лефёвр-Жино и итальянский натуралист Фабброни решили переопределить килограмм как массу литра воды, измеренную при \(4^{\circ}C\). Почему же именно при \(4^{\circ}C\), а не, скажем, \(3\) или \(5^{\circ}C\)? Дело в том, что именно при этой температуре вода обладает наибольшей плотностью. Таким образом, в \(1799\) году был изготовлен постоянный эталон килограмма из пористой платины, а спустя \(90\) лет был создан более точный эталон килограмма из платиноиридиевого сплава. Но каким бы точным ни был платиноиридиевый эталон, в \(2019\) году от него все же отказались.

Точный эталон килограмма образца \(1889\) года оказался не таким уж и точным. За \(100\) лет копии килограмма, разосланные по всему миру, подобно копиям прежде эталонного метра, неплохо “поднабрали” в массе – в среднем \(50\) микрограмм относительно главного эталона. Для ученых до сих пор остается загадкой, почему копии килограмма потяжелели, но ясно одно: для единицы измерения подобное поведение абсолютно непозволительно! Чтобы эталон килограмма впредь не изменялся, ученые решили дать новое определение килограмму через удовлетворительную постоянную. Новый килограмм оказался на распутье физического и химического путей определения.
Каков был возможный химический метод? Так сложилось, что единица измерения количества вещества «моль» (одна из семи основных единиц измерения в системе СИ) зависит от определения килограмма.
Количеством в \(1\) моль считалось количество вещества, содержащегося в \(12\) граммах изотопа углерод-\(12\). Согласно своему устаревшему определению, известная химическая константа Авогадро равна \(6.02214082(11)\cdot10^{23}\) атомам (именно столько атомов обозначается как \(1\) моль), содержащихся в \(12\) г этого изотопа углерода.
Простая логика говорила, что если число Авогадро зависит от килограмма, то можно сделать так, чтобы килограмм был определён через само число Авогадро! Чтобы вновь переопределить килограмм, ученым было необходимо вычислить точное число атомов в каком-нибудь физическом объекте.
Так начинается история о двух сферах, сделанных из изотопа кремний-\(28\). Сначала в Центральном конструкторском бюро машиностроения Санкт-Петербурга методом центрифугирования учёные выделили фторид кремния-\(28\). Затем полученный фторид кремния отправили в Институт химии высокочистых веществ, чтобы “взрастить” из него кристалл кремния. А уже в \(2007\) году в Институте выращивания кристаллов Лейбница (Leibniz-Institut für Kristallzüchtun) из данного кристалла взрастили пятикилограммовый цилиндр из чистого кремния-\(28\), которому придали форму шара и отполировали в австралийском Центр точной оптики (ACPO). Диаметр шаров составил \(93.75\) мм, а полировка была настолько точной, что если бы этот кремниевый шар был размером с нашу планету, то его самая высокая точка достигла бы высоты не более \(3\)–\(5\) метров. Таким образом, имея практически идеально круглый объект, можно с достаточной точностью рассчитать содержащееся в нём количество атомов. Приняв молярную массу кремния-\(28\) равной \(27.9769265325\) г/моль, а число Авогадро равным \(6.022 140 76\cdot 10^{23} \: моль^{-1}\), ученые определили массу килограмма как массу \(2.15\cdot 10^{25}\) атомов кремния-\(28\). Казалось бы, чем безупречно отполированная кремниевая сфера отличается от платиноиридиевого эталона килограмма? В отличие от сплава, утерянная или поврежденная сфера никаким образом не повлияет на определение килограмма, ведь масса \(2.15\cdot 10^{25}\) атомов кремния-\(28\) – определение фундаментальное.

Даже будучи чистейшим образцом, кремниевая сфера все же содержала некоторые примеси, а оксиды кремния и пыль прибавляли дополнительный вес эталону. Таким образом, и кремниевая сфера вскоре уступила более совершенному физическому методу определения килограмма (химический же метод, в свою очередь, пригодился для определения «моль» – единицы измерения количества вещества). Поэтому \(20\) мая \(2019\) года во Всемирный день метрологии было принято новое определение массы, привязанное к постоянной Планка. Более подробно о постоянной Планка вы можете узнать в статье "Я знаю, что ничего не знаю".
Вновь для переопределения килограмма перед учеными стояла задача точного определения самой постоянной Планка, чем и занялись сотрудники Национального института стандартов и технологий (NIST). С такой целью была использована установка, называемая весами Киббла. Весы состояли из двух чаш, на одну из которых подвешивался старый эталон килограмма, а на другую – обмотка с проводом длины \(L\), помещенная в магнитное поле \(B\). Если по проводнику будет идти электрический ток \(I)\, то магнитное поле будет взаимодействовать с проводником, образуя силу Ампера, уравновешивающую килограмм на другой чаше весов.
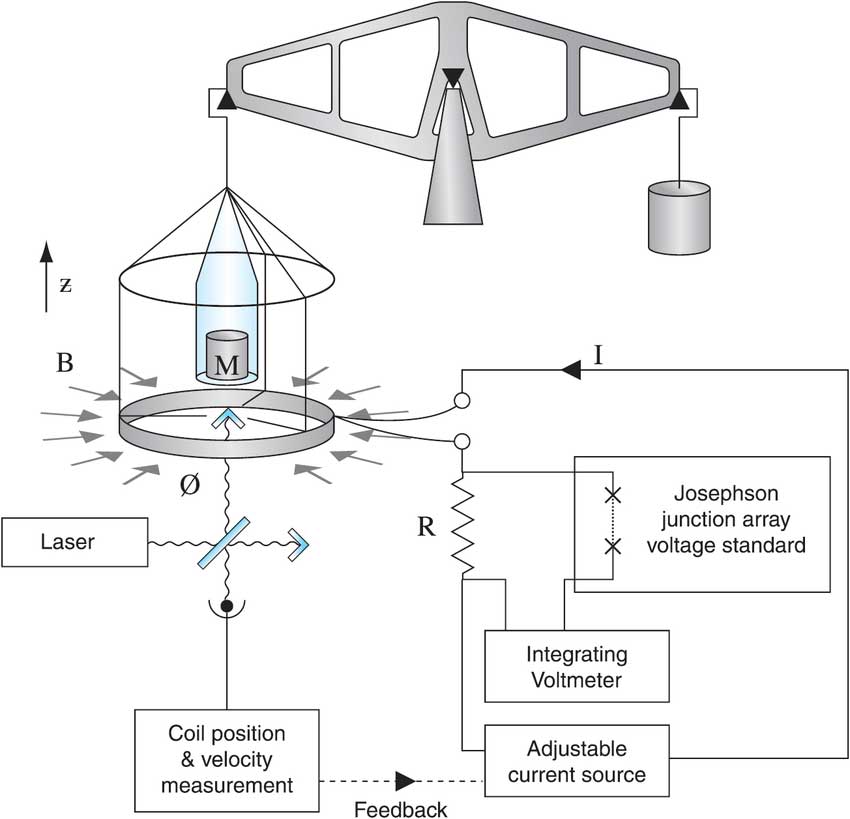
Для осуществления этого эксперимента и увеличения точности измерений применялись самые различные физические законы: сила Ампера, электромагнитная индукция Фарадея, квантовые эффекты Холла и Джозефсона. Не вдаваясь в подробности, приведём формулу вывода постоянной Планка \[h = \frac{4 g v}{p n^2 f^2} m\]Собрав необходимые данные с весов и используя данную формулу, исследователи смогли рассчитать значение постоянной Планка. Однако принцип работы весов Киббла оказался настолько сложен, что кремниевую сферу определили как вторичный эталон килограмма. Тем не менее ошибка весов в измерении константы была в несколько раз ниже, чем относительное расхождение масс физического эталона от его копий (порядка \(10^{-8}\))!
Отныне было решено: постоянная Планка однозначно равна \(h=6.62607015\cdot10^{-34}\: Дж\cdot с = 6.62607015\cdot10^{-34}\: кг\cdot м^2\cdot с^{-1}\), а килограмм получил своё фундаментальное определение через точную постоянную.

Кельвин
Что есть температура? Это степень того, насколько нагрето изучаемое тело. Первым измерять температуру начал Галилей, опустив перевернутую трубку в емкость с водой, как на изображении ниже. Принцип был довольно прост: поскольку давление газа напрямую зависит от температуры, при охлаждении вода тут же втягивается в трубку из-за атмосферного давления. Таким термоскопом можно было лишь сравнивать температуры, при этом не имея возможности количественно описать эту величину.
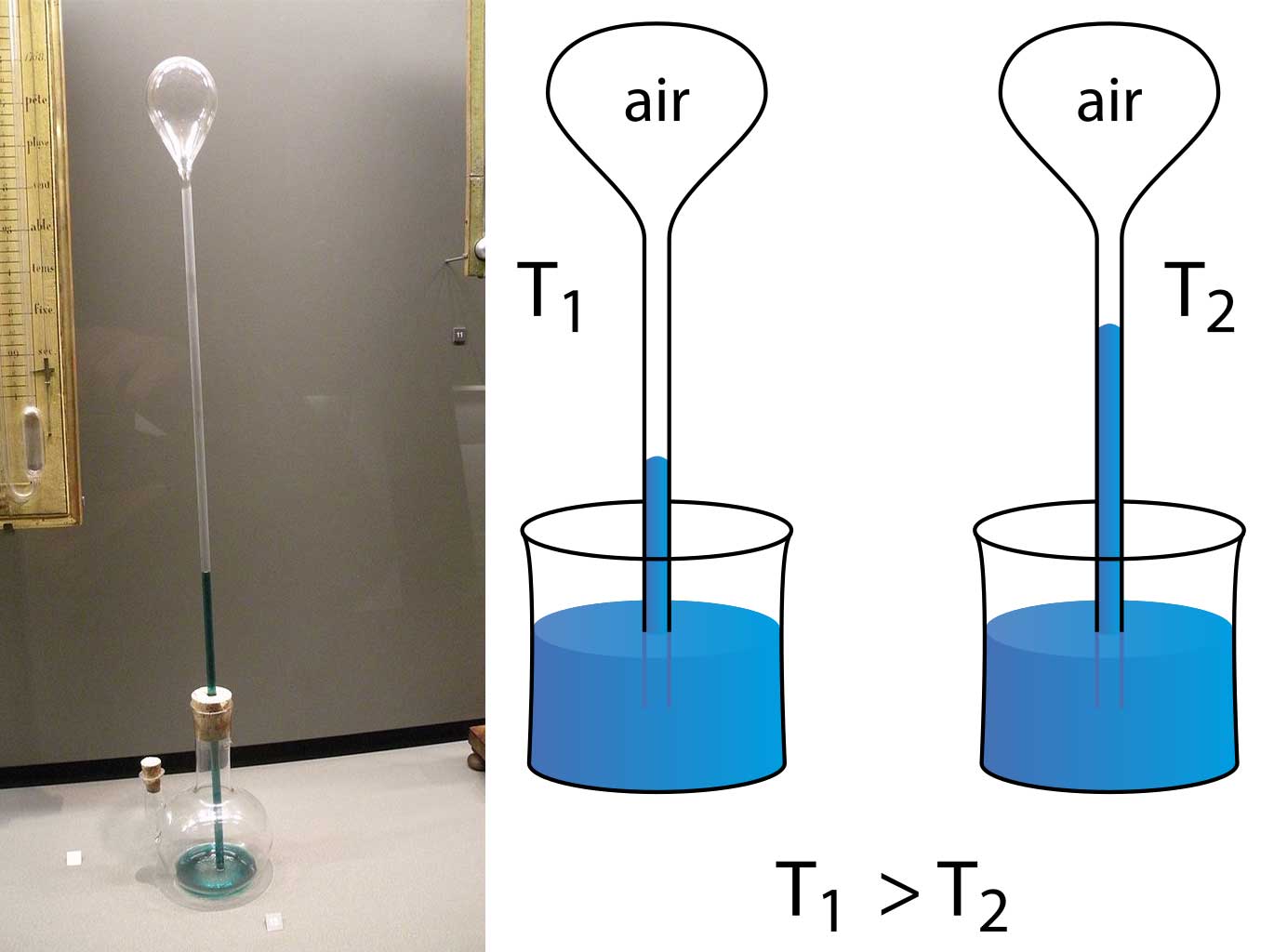
Со временем он стал совершенствоваться другими учёными, и первоначальный термоскоп трансформировался в первый прототип термометра: перевернув термоскоп шариком вниз, в него налили вещество, способное расширяться с повышением температуры. Появлялись и другие виды термометров вроде воздушного термометра Амонтона, основанного на упругих свойствах воздуха. Вот только современный вид термометры обрели лишь в \(1723\) году благодаря немецкому физику Фаренгейту, который также создал одноимённую шкалу, по сей день широко используемую в США. За нуль изначально была взята температура замерзания водного высококонцентрированного раствора хлорида аммония (рапа), а \(+96^{\circ}F\) – температура тела здорового человека.
В \(1742\) году другой ученый Андерс Цельсий предложил использовать шкалу, основанную на кипении и замерзании воды: за \(0\) он взял точку кипения, за \(100\) – точку замерзания воды, хотя позже шкалу решили перевернуть, сделав нулем точку замерзания воды. По наблюдениям Цельсия точка плавления льда не зависела от давления, а вот точка кипения зависела. Благодаря этим наблюдениям он впоследствии смог экспериментально определить точки кипения воды при различных значениях давления, на основе чего было выведено важное для термодинамики уравнение Клапейрона-Клаузиуса.
Век спустя лорд Кельвин доказал, что существует такая температура, при которой тепловое движение молекул полностью прекращается. Эта точка стала называться абсолютным нулём. После получения экспериментальных данных и теоретического расчёта на свет появилась абсолютная шкала Кельвина, основанная на шкале Цельсия: цена деления одинакова, но нуль по Кельвину смещён на \(273.15\) единиц относительно нуля по Цельсию.
Значение \(273.15\) К можно было получить в результате исследования с самой низкой погрешностью в термодинамике – определение давления и температуры тройной точки воды. Тройная точка – термодинамическое состояние, при котором некое вещество находится в трёх агрегатных состояниях одновременно.
Как такое возможно? Ранее мы упомянули, что Андерс Цельсий выяснил, что точка плавления льда не зависит от внешнего давления. На самом деле с повышением давления температура плавления все же линейно уменьшается, пусть и не очень быстро (точка плавления сдвигается на \(0.0072\) К с каждой атмосферой). Эту закономерность можно заметить в эксперименте по разрезанию льда. Если на большой блок льда в прохладном помещении подвесить медную проволоку с тяжёлыми грузами на её концах, то проволока начнёт медленно проходить сквозь лёд. В конечном счёте проволока должна разделить блок на две части, однако следа от неё не остаётся! Это объясняется тем, что очень тонкая проволока создаёт большое давление в несколько сотен атмосфер, и точка плавления льда снижается. Лед немного подтаивает от трения с проволокой. Затем давление возвращается в нормальное значение, и вода снова замораживается.
Перейдём к зависимости температуры плавления и кипения от давления. Ниже приведена фазовая P-T диаграмма для воды:
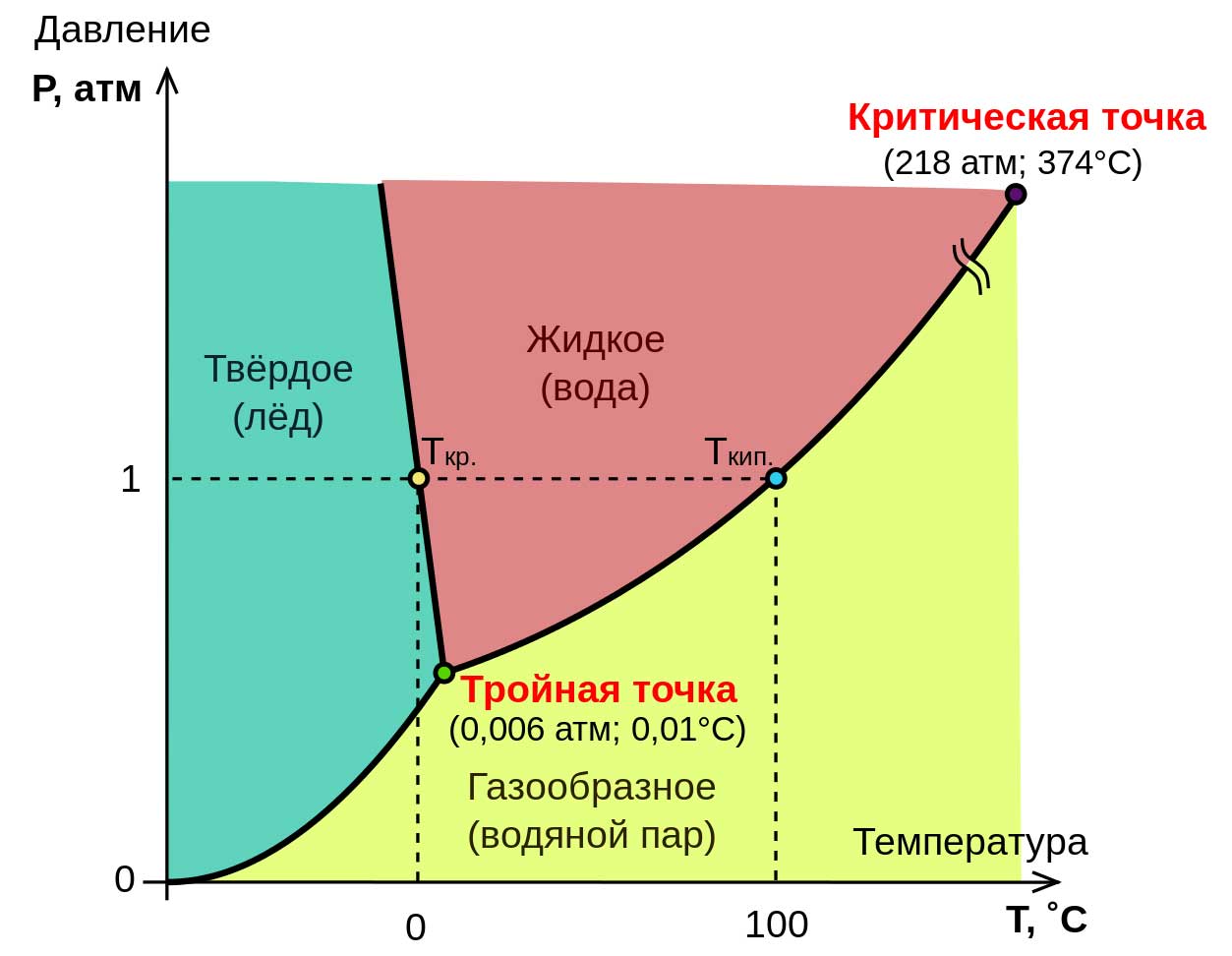
Можно заметить, что температура кристаллизации и кипения сходятся в тройной точке. Это состояние получается из единственной возможной пары значений давления (\(611.657\) Па) и температуры (\(0.01^{\circ}C\), что соответствует \(273.16\) К), поэтому данное состояние воды можно определить очень точно: в лабораторных условиях погрешность не превышает \(0.0001^{\circ}C\). Таким образом, в \(1954\) году Десятая генеральная конференция по мерам и весам утвердила: тройная точка воды точно равна \(273.16\) К, поэтому абсолютный нуль точно равен \(-273.15^{\circ}C\).
Казалось бы, температура обрела свою единицу измерения, а абсолютный нуль точно равен \(-273.15^{\circ}C\). Но не все так просто! Данный метод определения нулевой точки всё же даёт погрешности, проявляющиеся при высоких температурах. Ведущий научный сотрудник из Национальной физической лаборатории Соединённого Королевства Майкл де Подеста подтвердил нецелесообразность метода определения, основанного на тройной точке: «Когда измерения достигают \(1500^{\circ}C\), то, мягко скажем, глупо отталкиваться от тройной точки воды для измерения температуры». Он же предложил переопределить единицу «Кельвин» через точное определение постоянной Больцмана \(k\), константы, связывающей понятия температуры и энергии. Например, чтобы увеличить температуру одноатомной молекулы на \(1\) К, требуется \(\frac{3}{2}k\) Дж энергии.
И вновь физикам было необходимо точно вычислить значение постоянной, дабы привязать единицу измерения к незыблемой константе. Наполнив медный акустический резонатор заданным количеством аргона, Майкл де Подеста и его коллеги провели серию измерений скорости звука при различных частотах. Далее, основываясь на законах статистического распределения, они получили точную зависимость скорости звука от температуры газа, после чего наконец-то была выведена формула для нахождения постоянной Больцмана.:
\[k = \frac{\mu c^2}{\gamma N_A T}, \] где \(\mu\) – молярная масса аргона, \(N_A\) – число Авогадро, \(\gamma\) – показатель адиабаты, равный \(\frac{5}{3}\), c – измеряемая в ходе исследования скорость звука при температуре \(T\), \(T\) – температура аргона

Полученная формула не несет в себе неизвестных, все константы точно определены, благодаря чему постоянная Больцмана была благополучно рассчитана теоретически. Майкл де Подеста дополнительно рассчитал относительную ошибку своих измерений. Она составила \(7.1 \cdot 10^{-5}\%\), что составляет меньше одной миллионной доли! Благодаря этому постоянная Больцмана стала в точности равна \(k=1.380 649 \cdot 10^{-23} \: \frac{Дж}{К}\), и привязка Кельвина к этой константе отныне позволяет измерять температуру даже при её больших значениях. Вот так единица температуры прошла долгий путь до получения своего названия, своей шкалы и, самое главное, определения через константу!
Заключение
После определения основных единиц измерения их история развития пришла к своему логическому завершению. Метрология совершенствовалась под влиянием многих отраслей физики, от классической механики и термодинамики до физики элементарных частиц, при этом оставаясь верной основному принципу любой науки – поиску закономерностей и систематизации кажущегося хаоса в мироздании, а в основе точного описания законов природы лежит точность наших единиц измерений!
Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.
Редактор статьи: Дарина Мухамеджанова