[Математика ғажабы] Геометриямен жасырынбақ ойнау

Togzhan Shyntay

19 дек. 2021 г. • 8 мин. чтения

«Пән ғажабы неде» жобаның барлық мақалалары
«Математика ғажабы» циклдың басқа мақалалары
Визуалды дәлелдемелер
Байес теоремасы
Ойлаудың көркемдігі
Сымдарды кесеміз
Шексіздік
Пифагор теоремасы

Кез-келген геометриялық есепті аналитикалық жолмен шығаруға болады деп қабылданған. Шыныменде, егер сізде жеткілікті түрде тәжірибе болса онда сізге декарттық немесе бариентрлік координаттарды тұрғызу арқылы барлық геометрияны «сандар» арқылы оп-оңай шығарып (шығара алмауыңыз да мүмкін) тастау еш қиындық туғызбайды.

Бұл таңғаларлық нәрсе емес. Математиканы қаншалықты тереңірек зерттеген сайын, соншалықты оның түсініксіз немесе әр түрлі математика салаларының арасындағы шекаралардың бұлыңғыр екенін түсіне бастайсыз. Онда мынадай сұрақ туындайды: геометриялық емес есепті геометриялық жолмен шығаруға болады ма? Оның жауабы: иә, иә және тағы да иә!

Геометрияның басты ерекшелігі оның кез-келген есепті шығаруда әрқашан түсінікті бола алуы еді. Есептердегі геометриялық әдіс — бұл ұрпақтан-ұрпаққа беріліп келе жатқан мықты «құрал». Сонау ерте кездерде Wolfram Alpha (wolframalpha.com) мен Photomath сынды сиқырлы бағдарламалар болмағанның өзінде сол заманның адамдары көптеген математикалық амалдар мен олардың қасиеттерін геометриялық жолмен түсіндіріп бере алған.

Ал қазір төменде көрсетілген геометриялық емес есептерге сүңги отырып, олардың ішінде геометрияны іздеп көрейік!

X және Y? Бірінші бөлім

Егер \(\sqrt{x-1}+\sqrt{y-1}=1\) болса, \(\frac{x}{y}\) бөлшегінің ең кіші мәнін табыңыз.

Бір қарағанда, мұнда геометрияның бірде бір ізі жоқ секілді. Алайда, сізге бұл есепті геометриялық фигураны (жоқ, пентаграмманы емес) сызу арқылы шығара аласыз десем, онда бұл сөзім таза шындық болмақ.

Сол жақтағы өрнекке назар аударайық. Ол тек \( x \geq1\) және \( y \geq 1\) болған кезде ғана орындалады, себебі кері жағдайда түбір астында теріс мән болар еді. Сонымен қатар, әрбір түбірдің мәні \(1\)-ден аспауы керек, ал бұл дегеніміз \(x \leq 2\) және \(y \leq 2\).

\(x\) пен \(y\)-тің аралығын анықтауды аяқтаған соң бүкіл бағдарламаның түйініне, яғни берілген есептің геометриялық көрінісіне келейік.

Декарттық координаталар жүйесінде берілген теңдеудің графигін сызайық. Сонда ол \(ABCD\) шаршысында толығымен жатады.

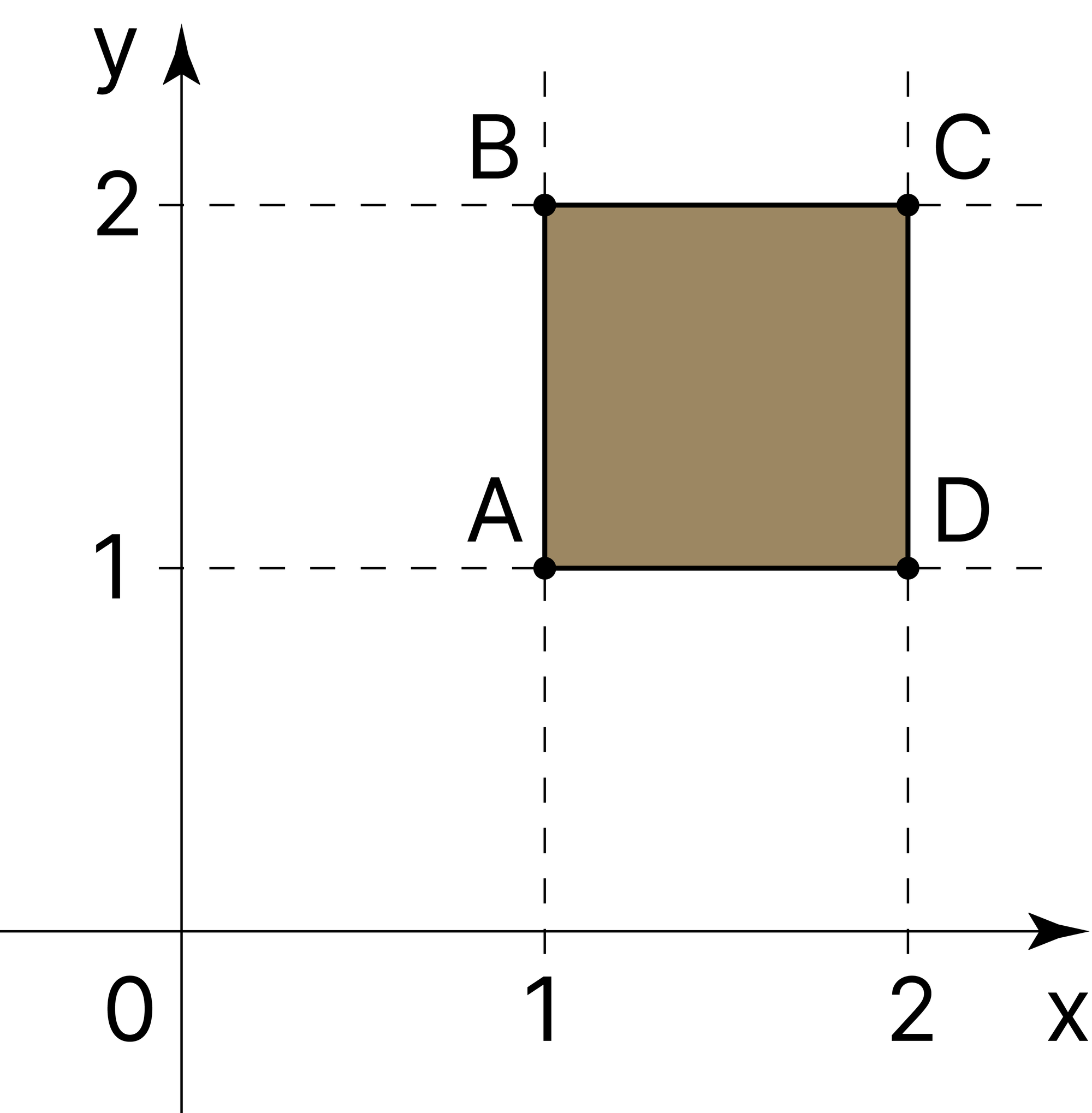
\(\frac{x}{y}\) бөлшегінің ең кіші мәні \(x\) ең кіші, ал \(y\) ең үлкен мәнді қабылдаған кезде ғана шығады. \(ABCD\) шаршысының барлық мүмкін нүктелерінен бұл шартты тек \(B(1; 2)\) нүктесі ғана қанағаттандыратыны көрініп тұр. Яғни берілген теңдеудің графигі \(B\) нүктесін қабылдайды, өйткені оның координаттарын теңдеуге қоятын болсақ, онда дұрыс бүтін санды теңдікті аламыз.

Яғни, жауабы \(\frac{1}{2}\)-ге тең деген сөз.

X және Y? Екінші бөлім

Қызығушылықтарыңыз оянды ма? Олай болса әрі қарай кеттік!

Берілген өрнектің ең кіші мәнін табыңыз: \(|x-y|+\sqrt{(x-3)^{2}+(y+1)^{2}} \)

Алдыңғы есептен түсінгендеріңіздей, бізде екі белгісіз айнымалы болған кезде декарттық кординаттада график тұрғызу өте ыңғайлы болады. Ал біз дәл қазір соны жасайын деп отырмыз.

Координаталық жазықтықта \(A (3; −1)\) нүктесі мен \(y=x\) түзуін қарастырайық. \(M(x; y)\) болсын, олай болса \(\sqrt{(x-3)^{2}+(y+1)^{2}} = MA\).

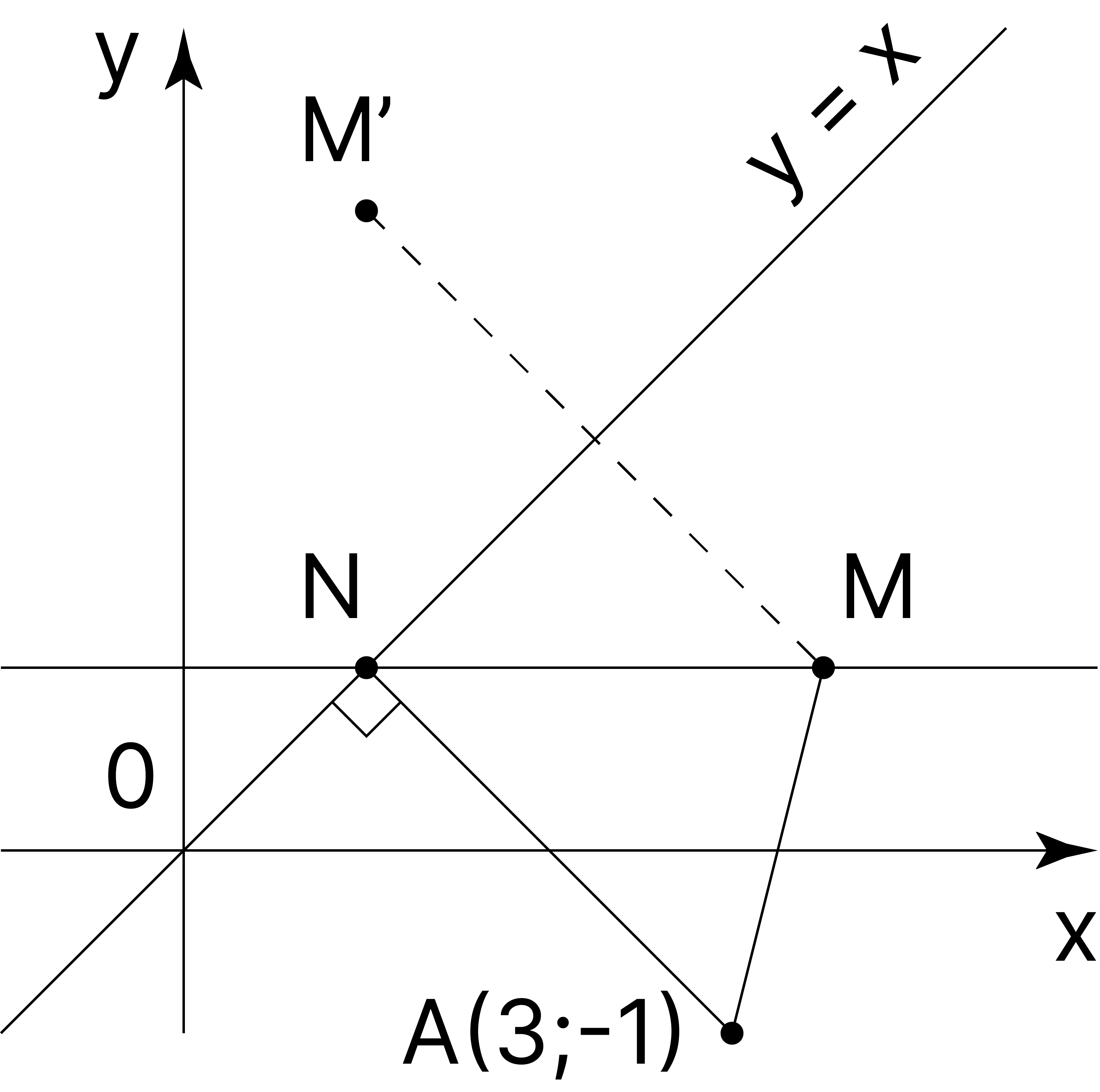
\(A(x; y)\) және \(B(m; n)\) нүктелерінің арасындағы қашықтық \(AB = \sqrt{(x-m)^{2}+(y-n)^{2}}\) формуласымен анықталатынын еске саламыз.

Егер \(M'\) нүктесі \(M\) нүктесіне \(y=x\) түзуіне қатысты симметриялы болса, онда \(M'(y; x)\) екенін байқаймыз. Олай болса бұл екі нүкте үшінде \(|x-y|\) өрнегі бірдей мәнді береді. Сондықтан \(А\)-дан есептегенде ең кіші арақашықтық \(А\) нүктесімен \(y=x\) түзуіне қатысты бір жарты жазықтықта жатқан нүктеде болады. Іздеп отырған \(M\) нүктеміз осы түзудің төменгі бөлігінде жатыр, сонда \(|x-y|=MN\) (\(N\) нүктесі дегеніміз \(y=x\) түзуінің \(M\) нүктесі арқылы өтетін горизонталь түзумен қиылысатын нүкте). Нәтижесінде \(MA+MN \geq AN\) үшбұрыштар теңсіздігінен \(M\) нүктесі \(AN\) кесіндісінде жатуы тиіс, ал \(AN\)-нің ең кіші мәні \(N\)-нің \(A\) нүктесінен \(y=x\) түзуіне түскен перпендикулярдің табаны болған кезінде ғана шығады.

Енді \(N\)-нің координатасын табу ғана қалды. \(y=x\) түзуінің бұрыштық коэффициенті бірге тең, сол себептен оған перпендикуляр \(AN\) түзуінің бұрыштық коэффициенті минус бір болады, яғни теңдеуіміз \(y=-x+c\) түрінде беріледі.

Егер екі түзу перпендикуляр болса, онда олардың бұрыштық коэффициенттерінің көбейтіндісі \(-1\)-ге тең болатынын еске саламыз.

Бұл түзу \(A (3; 1)\) нүктесі арқылы өтеді, сондықтан \(c=2\). Мына теңдеулер жүйесінің шешімі \(\left. \begin{cases} y=x, \\ y=-x+2 \\ \end{cases} \right.\) \(\left. \begin{cases} x=1, \\ y=1 \\ \end{cases} \right.\) болады, яғни \(y=x\) және \(y=-x+2\) түзулері \(N(1;1)\) нүктесінде қиылысады. Олай болса, онда \(AN = \sqrt{(1-3)^{2}+(1+1)^{2}} = 2\sqrt{2}\). Сондағы біздің іздегеніміз де осы еді!

Жауап: \(2\sqrt{2}\).

Байғұс Петяға көмектесейік

Жоғырадағы мысалдарда декарттық координатаны шебер қолдану арқылы алгебралық есептерді қалай шығаруға болатындығы айдан анық көрсетілген. Бірақ та тек осындай жағдайларда ғана геометрия бізге көмекке келмейді. Қанекей, геометриялық жолдың қолданылуының ең бір анық емес тәсілдерін қарастырайық.

Түсте Аннино мен Ванинодан Аня мен Ваня бір-біріне қарама-қарсы бағытта шығып, екі сағаттан соң кездесті. Сағат 14:00-де Аннинодан Петя шығып, бір сағаттан соң Аняны қуып жетті және де дәл осы сәтте Анниноға Ваня жеткен екен. Негізінде Петя тал түсте шығып, Ванямен кездесуді жоспарлаған. Сонда бұл кездесу қай уақытта болар еді?

Бұл есепте алдыңғы есептегідей бізді координаттар жүйесін тұрғызуға итермелейтін \(x\) пен \(y\) жоқ. Алайда есепте қозғалыс туралы айтылғандықтан оны график түрінде көрсетуге болатындығы бәріне түсінікті. Физиканың алғашқы сабақтарында болғандай уақыттың өтуіне тәуелді орын ауыстыруды көрсететін тікбұрышты координаталар жүйесін тұрғызайық. Аня, Ваня және Петяның қозғалыстарын \(AD, \ BN\) және \(PD\) сәулелері түрінде суретте көрсетілгендей етіп сызайық.

Суретте көрсетілгендей Аня, Ваня және Петяның әрекеттерін \(AD, \ BN\) мен \(PD\) сәулелері ретінде көрсетеміз.

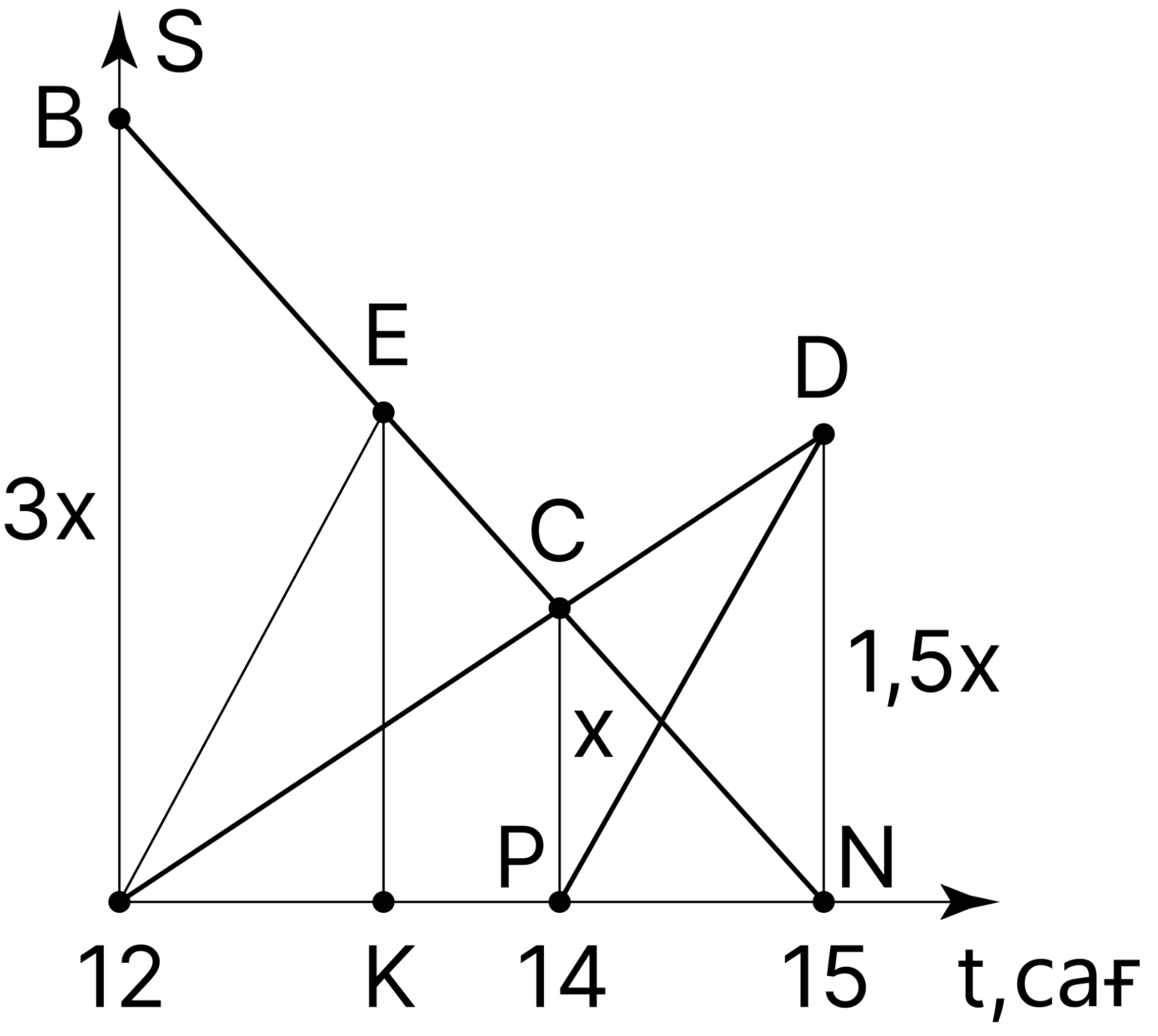
\(A\) мен \(B\) нүктесінің коорданаталары Аннино мен Ваниноның орналасқан жерін көрсетеді. Петя Аня секілді Аннинодан шыққандықтан, оның \(S\) осіндегі бастапқы координатасы нөлге тең. \(D\) нүктесінде Аня мен Петяның кездесуі өтті, ал \(C\) нүктесінде Аня мен Ваняның өткен. Егер Петя Анямен бір уақытта шықса, онда оның Ванямен кездесуі \(E\) нүктесінде болар еді. Есептің сұрағына жауап беру үшін \(t-K\) осіндегі \(E\) нүктесінің координатасын табу керек.

Петяның жылдамдығы тұрақты болғандықтан, \(AE\) түзуінің қозғалыс графигі \(PD\)-ға параллел болады. Бұлай болуының себебі: қозғалыс графигінің жылдамдығы градиент болып табылады.

Аня мен Ваня қозғалыстарын бастағаннан соң екі сағаттан кейін кездескен, яғни сағат 14:00-де. Біздің бақытымызға орай, дәл осы уақытта Петя өз қозғалысын бастады, ал бұл дегеніміз \(C\) және \(P\) нүктелерінің координаталары \(t\) өсіне қатысты бірдей және 14-ке тең. Оған қоса, Аня мен Петяның кездесуі Петя қозғалысын бастап, бір сағат өткен соң болды, яғни 15:00-де және де бұл Ваняның Анниноға дәл жеткен сәті. Олай болса, \(D\) және \(N\)-нің координаттары \(t\) осіне қатысты бірдей өзара тең. Осыған байланысты біз \(CP, \ DN\) және \(S\) осі өзара параллел болатындығын қуанышпен айта аламыз.

\(ACP\) және \(ADN\) үшбұрыштарын қарастырайық. Олардың ортақ \(A\) нүктесі бар және \(CP\parallel DN\), яғни бұл үшбұрыштар ұқсас. \(CP = x\) деп алатын болсақ, онда сол ұқсастықтан \(DN=1.5x\) екендігі шыға келеді.

\(S\) осімен \(CP\) параллель болғандықтан \(ABN\) мен \(PCN\) де ұқсас. Осыдан \(AB = 3x\) екендігі есептелді.

Мұның алдында біз \(AE\parallel PD\) екендігін айтып өттік. Енді осыны қолданайық! Олар параллель, сондай-ақ, \(EK\) және \(DN\) \(t\) осіне перпендикуляр, бұл дегеніміз \(EK\) және \(DN\) параллель! Демек, \(AEK\) мен \(PDN\) үшбұрыштары қандай? Дұрыс, олар да ұқсас!

\(k\) — дегеніміз \(AEK\) мен \(PDN\) үшбұрыштарының ұқсастық коэффициенті болсын. Онда \(AK = k\), \(EK = 1.5kx\). Егер \(BAN\) және \(EKN\) үшбұрыштарын қарастыратын болсақ, онда олардың ұқсас екенін байқау қиын емес. Осыдан келіп шығатыны: \(\frac{1.5kx}{3x} = \frac{3-k}{3}\). Бұл теңдеудің шешімі \(k = 1.2\) болады. Яғни, жоспарланған кездесудің уақыты — 13 сағат 12 минут.

X және Y енді жалғыз емес

Жоғарыда көрсетілген мысалдардан кейін геометриялық жолмен табылмайтын есептерде әрдайым координаталар жазықтығын қолдану үшін геометрия керек деген алдамшы сезім пайда болуы мүмкін. Алайда есептерді шығаруда координаталар жазықтығын қажет етпейтін өте көп, әртүрлі, әрі креативті геометриялық тәсілдер жетерлік және дәл қазір біз сондай мысалдардың бірін талқылайтын боламыз.

Егер \(0<x<1, \ 0<y<1, \ 0<z<1\) болса, онда \(x(1-y)+y(1-z)+y(1-x)<1\) екендігін дәлелдеңіз.

Қырының ұзындығы \(1\) болатын кубты қарастырайық. Бір төбеден шығатын қырларды таңдайық және олардың ұзындықтарын \(x, \ y,\ z\) болатындай етіп белгілейік.

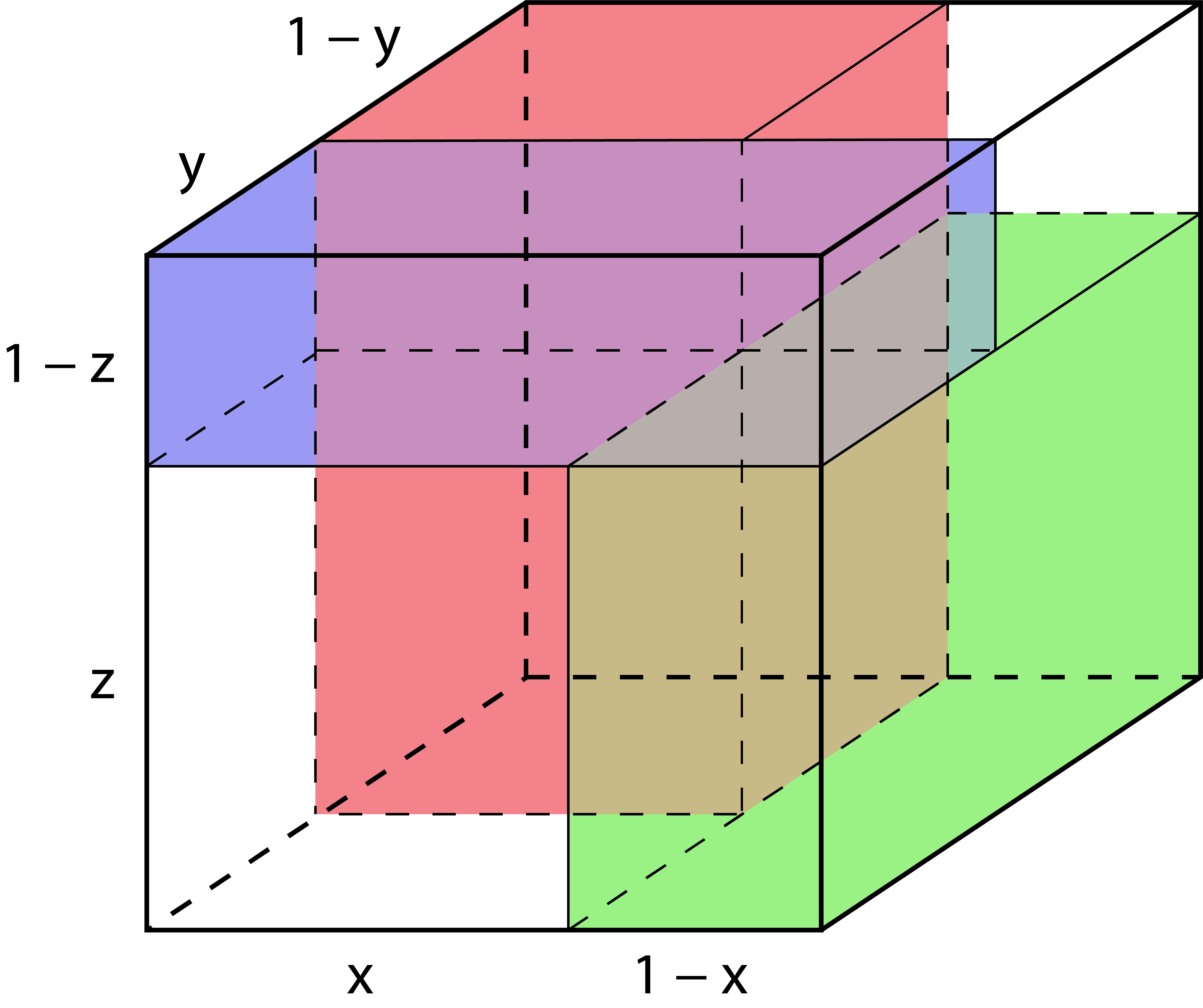
Өлшемдері \(x \times (1-y) \times 1\), \(y \times (1-z) \times 1\), \(z \times (1-x) \times 1\) болатын үш тікбұрышты параллелепид тұрғызайық. Бұл параллелепидтердің ортақ ішкі нүктелері болмағандықтан олардың көлемдерінің қосындысы бірден кіші болатыны анық. Олардың аудандары: \(x(1-y)\), \(y(1-z)\), \(z(1-x)\). Олай болса: \(x(1-y)+y(1-z)+z(1-x)<1\).

Нәтижесінде, өте ауқымды, қарапайым және күлкілі шешім шықты! Сіз осылайша геометриялық емес есептерді «әдеттен тыс» болып келетін тәсілдерді дұрыс қолдана отырып, шығара аласыз. Математиканың бөлек бөлімдері бар деген алаңдаушылықты шетке ысырып қойыңыз. Қаншалықты біртүрлі естілмесе де, математика — бұл ешқандай ережелері жоқ жер. Дәл осы жерде сіз тәжірибелер жасап, өзіңіздің тәсілдеріңізді де ойлап таба аласыз.

Лондонда ойнаймыз!

Геометрия тек қағазға жазылған есептерде ғана жасырынбақ ойнауды жақсы көрмейді, сондай-ақ, шын өмірде де жасырынуға дайын. Мұны тексеру үшін күні күркіреген Лондонның Әулие Павел шіркеуіне барайық.

Керемет шіркеудің дөңгелек галереясын бойлай серуендеп жүргенде бір-екі қадам басып-ақ сіз күтпеген жерден пайда болып, сол сәтте жоғалған әртүрлі дыбыстарға таңданып немесе тіпті үрейленіп қаларсыз. Сондықтан да бұл жерді «Демдер галереясы» деп те атайды. Сонымен бұл дыбыстарды естуге сізді не мәжбүр етеді? Рухтар? Елестер? Хогвортстан тыс сиқыр?

Негізінде бұл қарапайым математика ғана. Міне, осы жерде біздің геометриямыз тығылып жатыр. Іздеуге көшейік!

Сонымен сіз осы «сыбдыр эффекттісі» ғимараттың архитектурасына тікелей байланысты екенін түсініп қойған боларсыз. Қанекей, Әулие Павел шіркеуінің «Демдер галереясының» суретіне оның басты ерекшелігін байқау үшін көз салайық.

Өзіңіз көріп тұрғандай, бұл бөлме эллипс пішіндес. Осы пішіннің арқасында адамдар шіркеу ішіндегі сиқырға сеніп қалған.

Егер эллипс дегеніміз не деп іздейтін болсақ, онда келесідей анықтаманы көреміз:

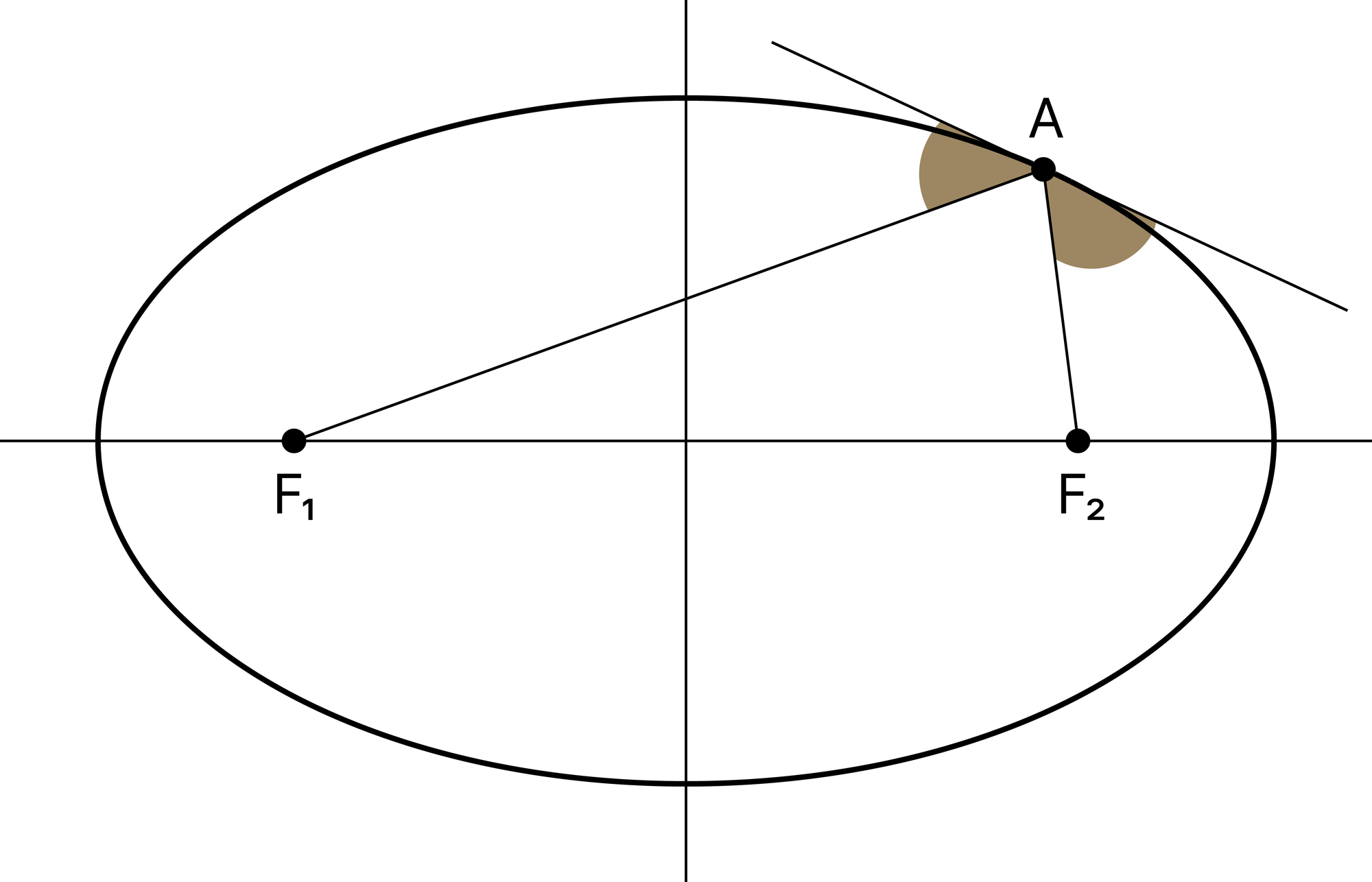
Эллипс — бұл әрбір нүктесінен \(F_1\) және \(F_2\) нүктелеріне дейінгі қашықтықтарының қосындысы әрдайым белгілі бір мәнге тең болатын тұйықталған жазық қисық. \(F_1\) және \(F_2\) нүктелері эллипс фокусы деп аталады.

Эллипстің анықтамасынан оның мынадай оптикалық қасиеті шығады: оның кез-келген нүктелерін фокустарымен байланыстыратын түзу осы нүктедегі жанамамен бірдей бұрыш жасайды. Сонымен қатар, сізге физикадан акустикалық дыбыстардың толқындары жарық сәулелері сынды эллипстің бір фокусынан шығып, екінші фокусында эллипстің қабырғасымен шағылысуының арқасында жиналатыны белгілі болар.

Эллипс пішінді бөлмелерде эллипстің бір фокусынды айтылған сыбыр, барлық бөлмеде емес, тек екінші фокусында ғана естілетін болады, тіпті, екі фокустың арақашықтығы біршама алыс болғанның өзінде де.

Осылайша біз геометрияны тағы да тауып алдық, оған қоса, эллипс пішінді бөлмелерде қалай өзге адаммен сыбырласуға болатындығын білдік. Сондықтан достарыңызбен қалжыңдасу үшін болашақ үйіңізді эллипс пішіндес етіп салуды жоспарлай берсеңіз де болады.

Көптеген адамдар геометрияның күшін өмірде қажет емес деп менсінбейді. Алайда шындығында, геометрия — тығылуды жақсы көретін математиканың момын мінезді бөлігі. Сондықтан геометрияның бар мағынасын түсіну үшін оны әрдайым іздеп отыруға тура келеді. Бұл іздеулер өте ұзақ, тіпті, күрделі болуы да мүмкін. Дегенмен геометриямен жасырынбақ ойнаудың ғажаптылығы есептің жауабын табуда емес, жауапты іздеу кезіндегі қызықты оқиғалар мен қиындықтарға толы болу үрдісінде жатыр. Әрине, бұл қиындықтардан сіз міндетті түрде өте алатын боласыз!

Пайдаланылған әдебиеттер:

А. Д. Блинков «Геометрия в негеометрических задач»

«Beyond Curriculum» қоры «Пән ғажабы неде» циклы материалдарын «Караван знаний» жобасымен серіктестікте және «Шеврон» компаниясының қолдауымен жариялауда. «Караван знаний» – жетекші қазақстандық және халықаралық сарапшылардың қатысуымен орындалған алдыңғы қатарлы білім тәжірибелерін зерттеу мен талқылау бойынша бастама.