Это какой-то неправильный треугольник!
Такой простой, но такой удивительный и полезный. Все эти прилагательные относятся к треугольнику Паскаля и его поистине магическим свойствам, о которых написано в этой статье.
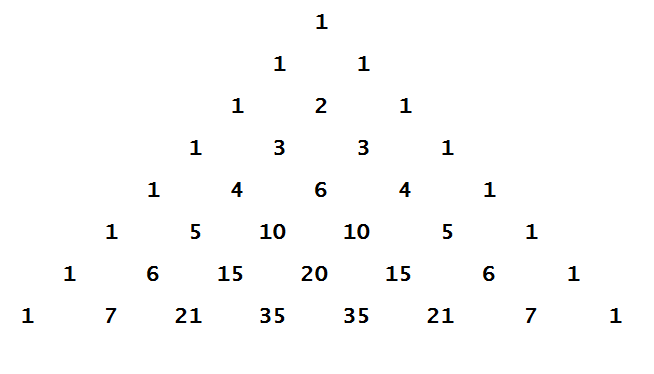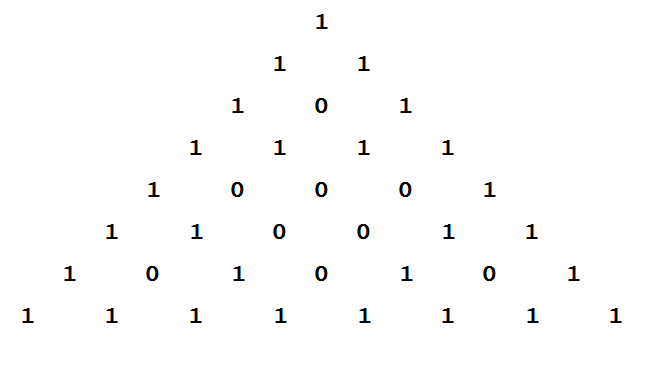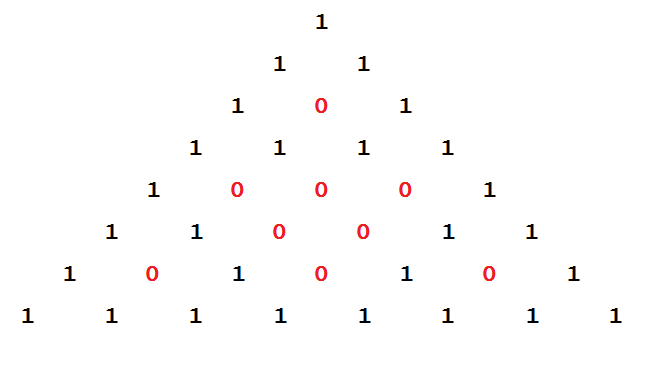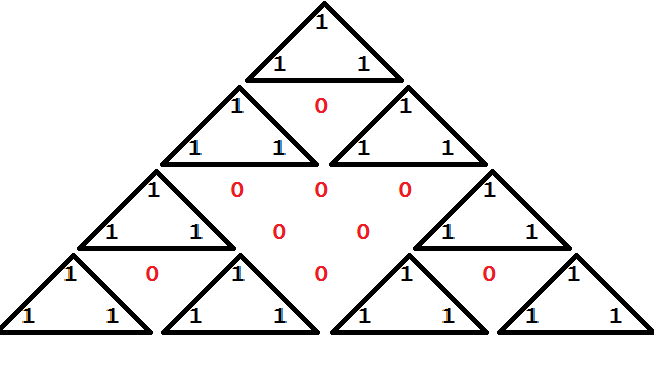
Эта статья является переизданием одноименной статьи из журнала Квазар от 15 января 2016 года. Многие авторы статей Квазара теперь являются участниками команды BeyondCurriculum и пришли к выводу, что некоторым людям может быть удобнее получать информацию в виде коротких статей онлайн. Если вы хотите получить полноценный опыт от чтения журнала, мы приглашаем вас скачать pdf с сайта Квазара.
Автор оригинальной статьи: Арман Болатов
Редактор переиздания: Владислав Черданцев

На первый взгляд может показаться, что перед нами просто аккуратно расставлен набор чисел, но на самом деле этот треугольник – неисчерпаемый источник математических радостей.
Своё название он получил благодаря французскому математику Блезу Паскалю. Это несправедливо по отношению к авторам трудов, которые были написаны несколькими столетиями ранее жизни Паскаля, так как сам француз, хоть и внёс несомненный вклад в развитие математики, все же не был в числе первооткрывателей треугольника.
Если коротко, то данный треугольник содержит в себе массу закономерностей. Начать следовало бы с принципа его построения: Возьмём число 1 и представим по обе стороны от него невидимые нули. Сложив их попарно, получим следующий ряд. Теперь повторим эту же операцию ещё раз. Повторяя в том же духе, у вас получится целочисленный треугольник Паскаля. Также просто можно объяснить устройство этого треугольника заметив, что каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес.
1. Так вот, каждая строка состоит из так называемых биномиальных коэффициентов разложения бинома \((a+b)^n\), где \(n\) – это номер ряда, а отчёт начинается с нуля. Итак если взять \(n = 3\) и разложить его в ряд, то получим: \(a^3+3a^2b+3ab^2+b^3\). При этом коэффициенты или числа перед переменными идентичны соответствующим цифрам в ряду треугольника Паскаля. Та же картина будет при \(n = 4\). То есть, треугольник Паскаля, это простой и быстрый способ определения всех таких коэффициентов.
2. Но это ещё не все. К примеру, сложив числа в каждом ряду, получим последовательные степени числа 2. Это происходит из-за следствия замены \(a\) и \(b\) на единицу, в формуле бинома описанной выше. Выполнив замену мы получим, что 2 в степени \(n\), равна сумме биномиальных коэффициентов \(n\) по \(k\). Или же сумме чисел ряда \(n\) в треугольнике Паскаля.
Представим каждое число в ряду в виде разрядов десятичной дроби. Другими словами, ряд номер 3 будет выглядеть так: \(1000 + 300 + 30 + 1\). Выполнив действия, получим число 1331, что, в свою очередь, является \(11^3\). Попробуем то же самое проделать с рядом номер 7. Вы получите сумму равную — 1,948,717, а это ничто иное как \(11^7\). Этот факт довольно легко обосновать, выполнив замену \(a\) и \(b\) на 10 и 1 соответственно в формуле бинома Ньютона, описанной пунктом ранее. Разложив полученный бином, мы получим выражение, равное сумме произведений биномиальных коэффициентов на \(10^k\), где \(k\) – номер элемента в ряду треугольника Паскаля.
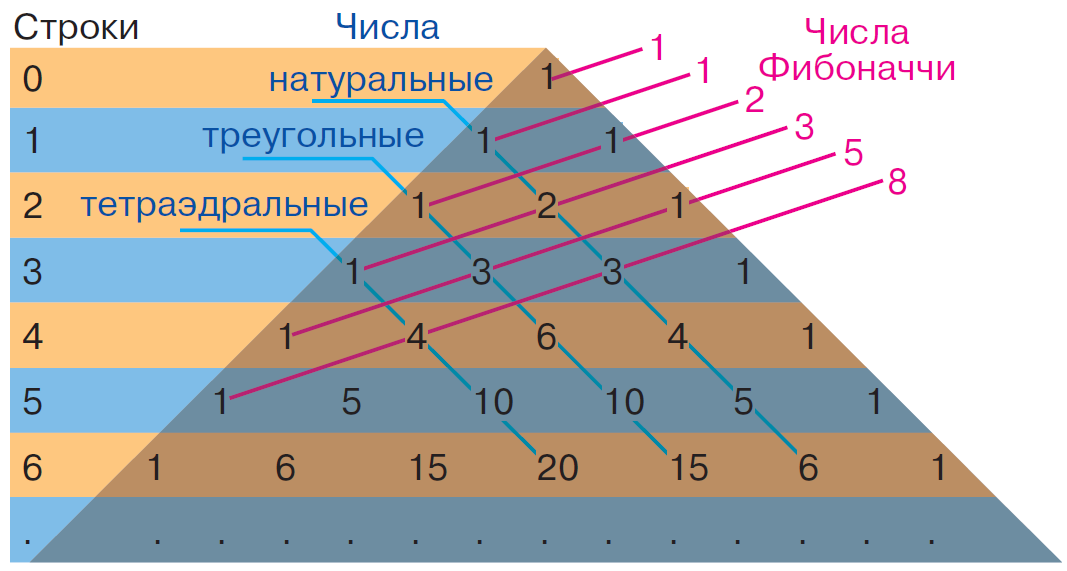
3. Кроме того, у треугольника имеются геометрические закономерности. Посмотрим на диагонали. Первые две не вызывают особенного интереса, сплошные единицы. А после, целые и положительные числа, известные как натуральные числа. Числа в следующей диагонали, называются треугольными, потому что из количества точек равного любому из чисел данной диагонали можно построить равносторонний треугольник.
Следующая диагональ состоит из тетраэдрических чисел поскольку, по аналогии с предыдущим пунктом каждое число равно количеству шариков, образующих тетраэдр, то есть один шар мы можем положить на три — итого четыре, под три подложим шесть (напрягитесь и представьте!) — итого десять, и так далее. А следующая диагональ продемонстрирует попытку выкладывания гипертетраэдра в четырёхмерном пространстве — один шар касается четырёх, а те, в свою очередь, десяти. В нашем мире такое невозможно, только в четырёхмерном, виртуальном. Пятимерный тетраэдр, о котором свидетельствует следующая диагональ, может существовать только в рассуждениях топологов.
А о чём же говорит нам самая верхняя диагональ, на которой расположились числа натурального ряда? Это тоже треугольные числа, но одномерные, показывающие, сколько шаров можно выложить вдоль линии. Если уж идти до конца, то самый верхний ряд из единицы — это тоже треугольные числа в нульмерном пространстве — сколько бы шаров мы не взяли — больше одного расположить не сможем, ибо просто негде — нет ни длины, ни ширины, ни высоты.
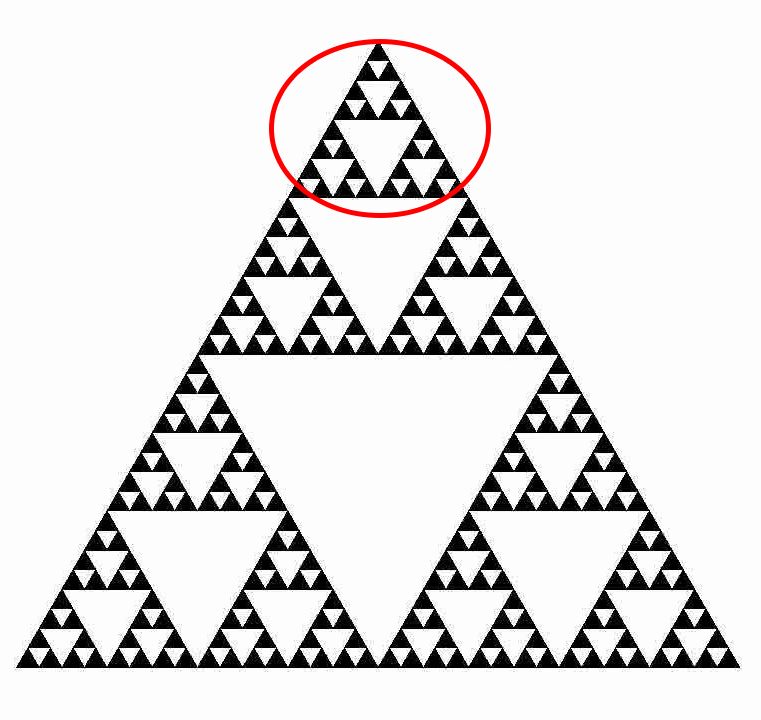
А как насчёт такого фокуса. Раскрасим все чётные числа в треугольнике в один цвет, а нечётные в другой. Тогда мы получим фрактал (множество, обладающее свойством самоподобия), известный как «треугольник Серпинского». Обоснованием этого факта является то, что если два подряд стоящих числа в треугольнике Паскаля имеют одинаковую чётность, то число стоящее под ними — четное. По аналогии, если два подряд стоящих числа разной чётности, то число под ними нечётное. Область, обведённая в красный круг подобна всему треугольнику.
4. Треугольник также полезен при вычислениях вероятностей в области комбинаторики. Скажем, вы хотите завести 3-х детей, и хотите просчитать вероятность что родятся два мальчика и одна девочка. В уравнении оно примет вид \((Мальчик+Девочка)^3\). Теперь посмотрим на третий ряд, где первое число соответствует трём мальчикам, а последнее трём девочкам. А вот второе число в этом ряду соответствует двум мальчикам и одной девочке как раз то что мы искали: 3 делим на сумму всех вероятностей в ряду. Стало быть, интересующая нас вероятность равна \(\frac{3}{8}\) или 37.5%.
Ещё один пример: Представим, что вы случайным образом выбираете из десяти друзей, волейбольную команду, состоящую из четырёх игроков. Так вот, сколько вариантов групп у вас может получиться? В комбинаторике, эта задача будет звучать как размещение из 10 по 4. И высчитывается по этой формуле \[ { n \choose k } = \frac{n!}{(n-k)!k!}= \frac{10!}{6!4!}=210 \] Но достаточно взглянуть на 4-й элемент 10-го ряда нашего треугольника, и мы получим ответ.
Другой пример: предположим, что некий шейх, следуя законам гостеприимства, решает отдать вам трёх из семи своих машин. Сколько различных выборов вы можете сделать среди прекрасных представительниц гаража? Для ответа на этот волнующий вопрос необходимо лишь найти число, стоящее на пересечении диагонали 3 и строки 7: оно оказывается равным 35. Если, охваченные радостным волнением, вы перепутаете номера диагонали и строки и будете искать число, стоящее на пересечении диагонали 7 со строкой 3, то обнаружите, что они не пересекаются. То есть сам метод не даёт вам ошибиться!
Какие ещё открытия ждут нас впереди, решать вам.
