[Прелесть математики] Бесконечность

Все статьи из цикла "В чем прелесть предмета"
Другие статьи из цикла "В чем прелесть математики":
  Визуальные доказательства
  Теорема Байеса
  Красота рассуждений
  Режем провода
  Прятки с геометрией
  Теорема Пифагора

Все мы знаем, как ведет себя математика, когда мы используем обычные арифметические операции вроде сложения или умножения со знакомыми нам действительными числами. Однако математика становится куда более интригующей, когда числа кончаются и начинается бесконечность…

Бесконечность в математике имеет куда большую роль, чем можно себе представить: будучи значимой частью многих разделов математики, порой бесконечность способна привести нас к невероятно красивым решениям.

Парадокс “Гранд-отель”

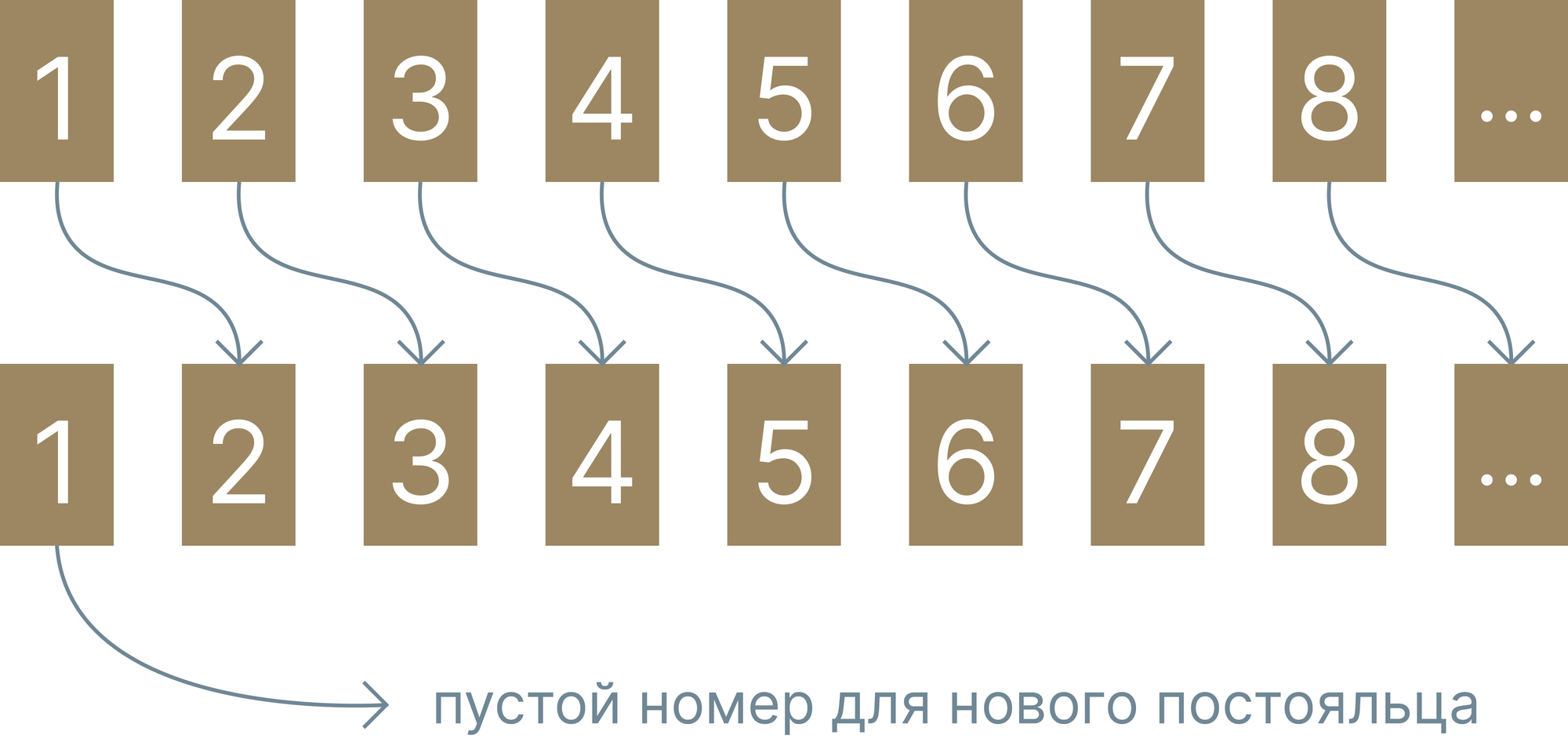
Представьте отель с бесконечным числом номеров, при этом во всех его номерах уже есть постояльцы. Вдруг появляется еще один гость, желающий заселиться в отель. Как вы думаете, что сделает администрация отеля? Удивительно, но они ему не откажут! Администрация всего лишь попросит постояльца первого номера поселиться во второй, второго – в третий, третьего – в четвертый и так далее. Число номеров бесконечно, а значит место всегда найдется.

Замечательность замечательных пределов

Рассмотрим другой пример, который звучит более реально. Представьте, что вы решили открыть депозит в банке с определенным процентом. С течением времени начальная сумма депозита возрастает согласно процентным ставкам. Ваши деньги “растут” каждый месяц, скажем, на \(10\%\), и через год после открытия вклада накопленная сумма увеличится в \(1.1^{12}=3.14\) раз (число похоже на \(\pi\), но это лишь совпадение). Попробуем выразить формулу зависимости размера счета на депозите от времени. Пусть \(P(t)\) – сумма на депозите через \(t\) месяцев, а \(x\) – изначальный вклад.

Воспользуемся примером с \(10\%\) и за изначальную сумма вклада возьмем \(100\) тенге. Таким образом получается:\[P(0) = 100\] \[P(1) = 100 + 100\cdot \frac{1}{10}=100\left(1+\frac{1}{10}\right),\] так как сумма увеличилась на \(10\) процентов, а \(10\%\) – это одна десятая часть. Теперь вычислим значение \(P(2)\):\[P(2) = 100\left(1+\frac{1}{10}\right) + 100\left(1+\frac{1}{10}\right)\cdot \frac{1}{10}=\]\[= 100\left(1+\frac{1}{10}\right)\left(1+\frac{1}{10}\right)=\]\[= 100\left(1+\frac{1}{10}\right)^2\]Если подобную операцию повторить для следующих временных промежутков, то можно заметить, что аргумент нашей функции (количество прошедших с открытия депозита месяцев) совпадает с показателем степени выражения в скобках, то есть функцию можно записать в общем виде:\[P(t)=x\left(1+\frac{1}{10}\right)^t\]Теперь немного изменим условие. Пусть размер депозита будет увеличиваться не один раз в месяц, а два раза в месяц, и не на \(10\%\), а на \(5\%\). В этом случае функция изменяется и превращается в:\[P(t)=x\cdot\left(1 + \frac{1}{20}\right)^{2t}\]В данной функции \(1 + \frac{1}{20}\) показывает, что каждый месяц сумма увеличивается на \(5\%\), а \(2t\) означает, что частота пополнения депозита увеличилась до \(2\) раз в месяц. Есть ли разница между этими двумя функциями? К примеру, вы с другом положили на депозит \(1000\) тг, но ваш друг положил их с условием из первой функции, а вы – из второй. У кого будет больше денег на депозите через \(5\) лет? Поздравляю, именно вы получите большую прибыль! Почему же так происходит? Это покажется на первый взгляд странным, но вторая функция растет быстрее, чем первая. Таким образом, если сумма вашего депозита будет увеличиваться чаще, то денег на вашем счету будет явно больше, несмотря на то, что увеличивается депозит на меньший процент.

Однажды ученые задумались: что если сумма на депозите будет увеличиваться бесконечное число раз в месяц на бесконечно малое число процентов – какая будет прибыль? Используя логику из предыдущего примера, мы можем сделать вывод, что в таком случае функция будет выглядеть так:\[P(t)=x\cdot (1+\frac{1}{n})^{nt},\]где число \(n\) показывает, во сколько раз изменяется частота увеличения депозита за месяц, а \(\frac{1}{n}\) показывает бесконечно малый процент депозита, так как \(n\) стремится к бесконечности. Но нам интересна не сама сумма, а лишь то, во сколько раз она будет увеличиваться за месяц, поэтому мы немного упростим выражение и запишем его в виде предела:\[\lim_{n \to \infty} (1+\frac{1}{n})^n\]

Что означает данная запись? Только то, что каждый раз вместо \(n\) в формулу мы будем подставлять какое-то очень большое число. Давайте теперь узнаем, чему равно это выражение.

Подставим вместо \(n\) большое число, скажем, миллион. Что получается? Если посчитать на калькуляторе, то выйдет:\[\left(1+\frac{1}{1000000}\right)^{1000000}=2.71828\]Попробуйте использовать число побольше. Вскоре вы заметите, что калькулятор будет давать одно и то же число – это приблизительное значение постоянной Эйлера. Точное значение мы получим лишь в том случае, если \(n\) станет действительно бесконечным. А теперь задумайтесь: при возведении некого числа, большего единицы, в бесконечную степень результат не превышает трех. Это ли не замечательно!

Такой предел называется вторым замечательным пределом.

Пока что мы опустим его доказательство и перейдем к первому замечательному пределу:\[\lim_{n \to 0} \frac{\sin(n)}{n}, \: (n\:в\:радианах) \]

В этом пределе \(n\) вместо бесконечно большого числа принимает наоборот бесконечно малые значения, близкие к \(0\) (но не равные ему!).

Попробуйте самостоятельно доказать его! Если вы почувствуете, что вдруг застряли в дебрях доказательства, ниже мы даем пошаговые инструкции к одному интуитивному доказательству этого предела:

\(1\). Нарисуйте окружность с радиусом \(1\) и центром \(O\).

\(2\). Проведите \(2\) радиуса \(OA\) и \(OB\).

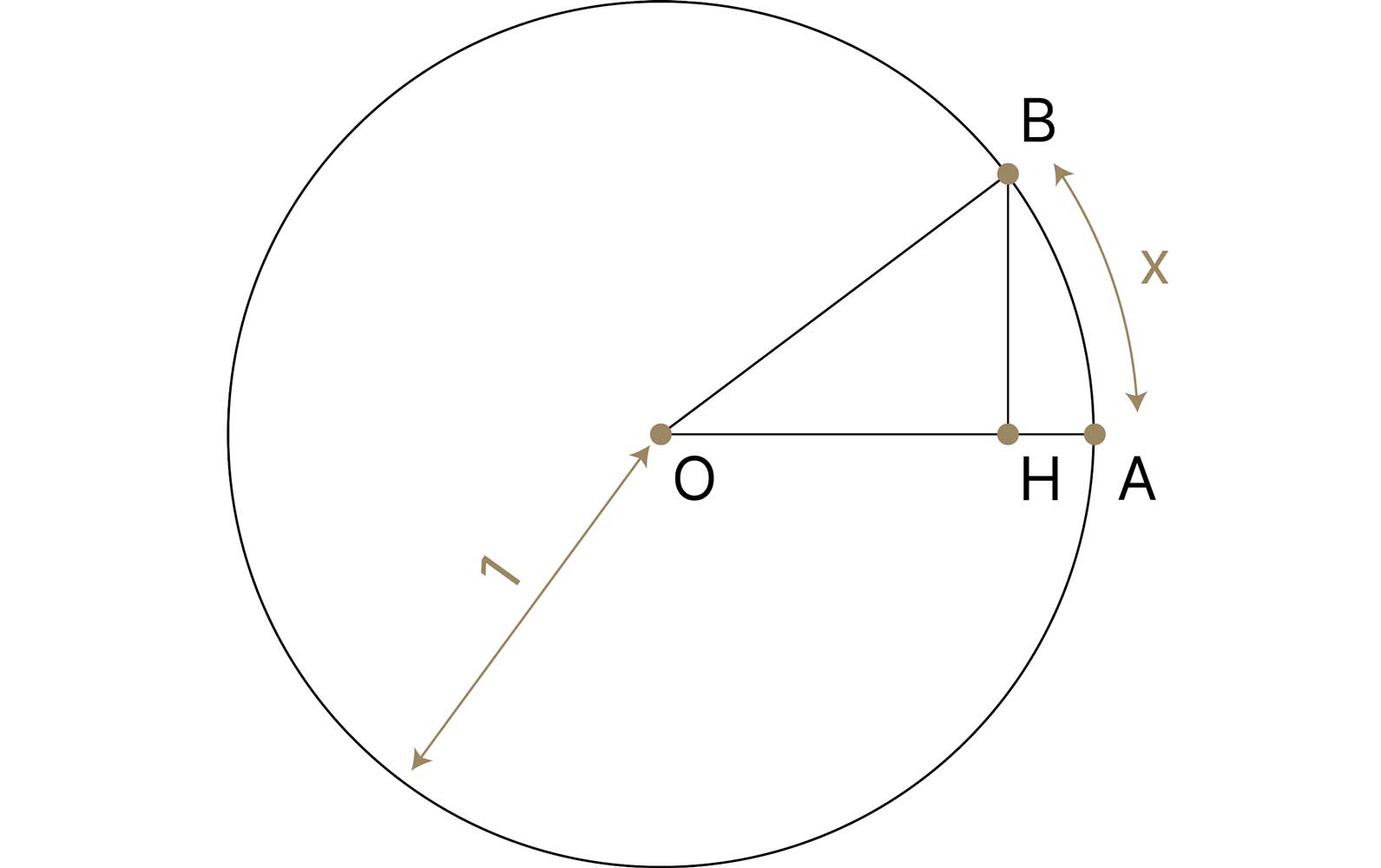
\(3\). Чему равна дуга \(AB\)? А чему равен синус \(\angle AOB\)? Какая между ними связь?

\(4\). Ответы на вопросы выше: если длина дуги равна \(x\), то \(\angle AOB\) равен \(x\) радиан, а \(sin(x)\) равен высоте, опущенной из точки \(B\) на \(OA\).

\(5\). Заметим, что чем меньше \(\angle AOB\), тем ближе длины дуги и высоты, а следовательно, сравниваются \(x\) и \(sin(x)\).

Парадоксы с бесконечными числовыми рядами

Порой работа с бесконечностями может привести нас к различным парадоксам. В качестве примера возьмем бесконечную сумму:\[1-1+1-1+1-1+1-1+\dots \]Попробуем поставить скобки так, чтобы каждая скобка давала \(0\):\[(1-1)+(1-1)+(1-1)+(1-1)+\dots\]Если следовать подобной логике, ответ очевидно равен \(0\). А что если решить эту задачу немного иначе? Снова расставим скобки, но немного по-другому. Пусть первое слагаемое останется без компаньона, тогда выйдет: \[1-(1-1)-(1-1)-(1-1)-\dots\]В этом случае первое слагаемое равно \(1\), а остальные – \(0\), а значит конечная сумма уже равна \(1\).

Решим задачу еще раз, но снова немного перепишем сумму. Пусть второе слагаемое встанет на место первого, третье – на место второго, четвертое – третьего и так далее, а первое же слагаемое встанет на последнее место (как в примере с бесконечным отелем). Расставим скобки, вновь оставив первое число без пары:\[-1+(1-1)+(1-1)+(1-1)+\dots\]Получается, что первое слагаемое равно \(-1\), а остальные – \(0\), то есть общая сумма будет равна \(-1\).

Теперь обозначим эту сумму за \(S\) и посмотрим, чему равно значение \(1-S\):\[S =1-1+1-1+1-1+1-1+\dots\]\[1-S=1-(1-1+1-1+1-1+\dots)=\]\[=1-1+1-1+1-1+1-1+1-1+\dots\]Выходит, что значение \(1-S=S\). Удивительно! Похоже на линейное уравнение, которое можно решить и получить \(S=0.5\).

Так к чему приведет данная бесконечная сумма? \(0, 1, -1\) или \(0.5\)? На самом деле, ни одно из этих решений не будет верным, так как подобная сумма называется расходящейся. Иначе говоря, невозможно найти конечное числовое значение данной суммы, что и приводит нас к разным результатам. Попробуйте понять, какие из следующих рядов приведут нас к определенному конечному значению (сходятся), а какие расходятся:\[1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\dots\]\[1+2+4+8+16+32+64\]\[\frac{1}{2}-\frac{1}{3}+\frac{1}{4}-\frac{1}{5}+\frac{1}{6}-\frac{1}{7}+\dots\]

Сравнение бесконечностей

Задумывались ли вы когда-нибудь, чего больше: натуральных или целых чисел? Логичный ответ – целых чисел, так как целые числа включают в себя и натуральные. Но не стоит забывать, что каждое из этих множеств бесконечно! Давайте вспомним, что натуральные числа – это именно те числа, которые мы используем для подсчета и нумерации элементов (\(1, 2, 3, 4...\)). Поэтому, чтобы ответить на этот вопрос, нужно задать другой: сможем ли мы пронумеровать каждое из целых чисел? Давайте попробуем это сделать! Пусть каждое отрицательное число будет под четным номером, например \(-1 \rightarrow 2, -2 \rightarrow 4\) и так далее. То есть номер \(N(x)\) отрицательного числа \(x\) вычисляется как \(N(x) = -2x\). Тогда положительные числа и нуль будут нечетными натуральными числами, например \(0 \rightarrow 1, 1 \rightarrow 3, 2 \rightarrow 5\) и так далее. Получается, что \(N(x) = 2x + 1\), если \(x ≥ 0\). Так для каждого целого числа есть соответствующее ему натуральное число. Данный факт доказывает равенство количества элементов (мощность) в данных множествах.

Получается, мощность множества натуральных чисел равняется мощности множества целых чисел. Другими словами, множество целых чисел счетно, так как к каждому целому числу можно назначить соответствующее натуральное число, а следовательно, можно и посчитать их. Не менее интересно, что множество рациональных чисел тоже является счетным. Чтобы проиллюстрировать справедливость данного утверждения, достаточно взглянуть на картинку.

Видно, что красной стрелочкой можно пройтись по каждому рациональному числу, последовательно пронумеровав их натуральными числами, что показывает равенство мощности множеств рациональных и натуральных чисел.

Для измерения мощности множеств используются кардинальные числа. К примеру, мощность натуральных чисел – это אo (алеф-ноль). Следующее кардинальное число всегда больше предыдущего. Это означает, что существует бесконечности, большие других бесконечностей.

Вот так простое рассуждение об основах математики привело нас к другим ранее неизведанным видам чисел – кардинальным.

Заключение

В математике она – прима-балерина, она играет главную роль и может привести нас в совершенно неожиданные места. Она способна создать множество парадоксов, и при этом она же способна их разрешить. Она таинственна, и невероятно прекрасна. И имя ей бесконечность.

Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.

Редактор статьи: Дарина Мухамеджанова