[Прелести математики] Красота рассуждений
В этой статье мы расскажем о красотах математических рассуждений и покажем, почему же именно они достойны называться главной чертой самой математики.
![[Прелести математики] Красота рассуждений](/content/images/size/w2000/2020/12/math-wallpaper-119---3264x2448.jpg)
Все статьи из цикла "В чем прелесть предмета"
Другие статьи из цикла "В чем прелесть математики":
Визуальные доказательства
Теорема Байеса
Режем провода
Прятки с геометрией
Бесконечность
Теорема Пифагора
«Правильный взгляд на математику открывает не только истину, но и безупречную красоту — холодную и суровую, как скульптура, отстранённую от человеческих слабостей, лишённую вычурных уловок живописи и музыки — горную кристальность и строгое совершенство великого искусства»
— Бертран Рассел
Семь мостов Кеннигсберга

В восемнадцатом столетии в Восточной Пруссии на берегу реки Прегель стоял славный город Кенигсберг, нынешний Калининград. Кнайпоф, Альтштадт, Ломзе, Форштадт – четыре части города связывались семью мостами. Прогуливаясь по бесконечным улочкам Кенигсберга, горожане задавались вопросом: можно ли вернуться в исходную точку в любом месте города, пересекая каждый мост лишь единожды? Так и звучит известная головоломка о семи мостах Кенигсберга. Нельзя не отметить удивительное сходство данной головоломки с дублинской, где спрашивается можно ли пройти из одной части Дублина в другую, не проходя мимо паба.

В математике для решения подобных задач удобно абстрагироваться. Для этого давайте заменим части города на точки, мосты на линии, а названия самих частей на \(A\), \(B\), \(C\), и \(D\). Получится следующая картина:
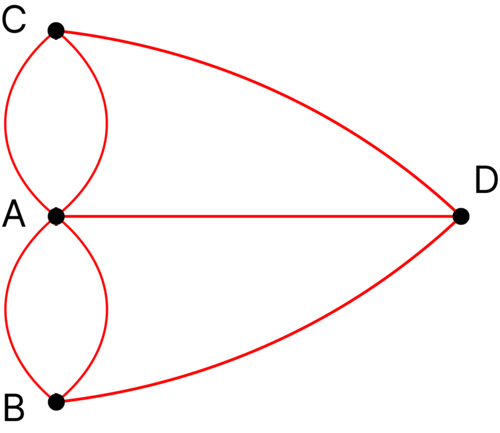
Предположим, что наша отправная точка есть точка \(A\). Эйлер заметил, что для того, чтобы возвратиться в исходную точку, при этом пройдя каждый мост лишь единожды, необходимо знать точное число мостов, связанных с отправной точкой \(A\).
Чтобы начать наше путешествие от точки \(A\) и вернуться туда же, необходимо покинуть точку \(A\) на каком-то мосту, затем вернуться к \(A\) с другого моста, затем вновь покинуть и так снова и снова. Отсюда видно, что все ведущие в \(A\) мосты разбиваются на пары, состоящие из входящих и исходящих мостов. Однако из схемы видно, что с точкой \(A\) связано нечётное число мостов, а значит один мост останется без пары. Следовательно, отправившись в путь с подобного «одинокого» моста, горожанин Кенигсберга не смог бы вернуться на точку \(A\). Стало быть, коль число мостов нечётное, невозможно выйти из точки \(A\) и вернуться туда же – не достаёт одного моста. Данное доказательство применимо не только к условной точки \(A\), но и к остальным точкам или же частям города, так как и они связаны нечётным числом мостов.
Решение Эйлера – известный пример элегантного доказательства в истории математики. Его решение, казалось бы, тривиальной головоломки привело к зарождению совершенно новой области математики, называемой теорией графов, без которой не обойтись для понимания и проектирования телекоммуникационных сетей, компьютерных схем, сложных расписаний и многого другого.
Столкнувшись с головоломкой о семи мостах Кенигсберга сегодня, многие ученые-математики посчитали бы более рациональным использовать компьютер для построения многомиллионных вариантов маршрута, нежели решать головоломку вручную. Конечно же, в итоге компьютер бы пришел к выводу, что невозможно вернуться в исходную точку, пройдя через каждый мост лишь единожды, выведя на экран однозначное «невозможно». Но разве обладают громоздкие, лишенные ясности и некой артистичности решения компьютера... элегантностью? Могут ли они объяснить почему же невозможно, а уж тем более привести к новым, смелым идеям и внезапным озарениям? Подход Эйлера, напротив, не только предоставляет ответы на многочисленные «почему», но и открывает дверь в новый, удивительный мир теории графов, появившейся благодаря математику, решившему «поломать» мозг над головоломкой семи мостов Кенигсберга. Оно и к лучшему, однако, что Эйлер не застал появление первого компьютера!
Метод Гаусса

В конце 18 века немецкий мальчик Карл Гаусс оказался на своем первом уроке арифметики. Вдруг учителю понадобилось оставить класс учеников на короткое время. Решив занять юных непосед, учитель предложил необычную задачу – сложить все числа от 1 до 100. Только учитель собирался переступить порог класса, молодой Гаусс поднял руку, закончив решать сложную задачку. Будущий ученый-математик заметил, что: \(1 + 100 = 101\), \(2 + 99 = 101\), \(3 + 98 = 101\), \(\dots\), \(50 + 51 = 101\), поэтому сумма всех чисел от 1 до 100 равно произведению 50 на 101, что составляет 5050!
Гаусс сумел метко использовать симметрию чисел, так плавно работающую в самой задаче. Очевидно, что поочередно считать \(1 + 2 + 3 +\dots\) займет много больше времени чем если разбить числа на пары, все становится намного проще и яснее.
Разумеется, оба подхода дадут один и тот же ответ, но решение Гаусса емкое и элегантное, а другое длинное и труднорешаемое. Подход Гаусса также намного более действенен и универсален, чем прямой подсчет, так как идея симметрии не привязана именно к этой задачи, а значит может быть использована для решения других более сложных. Еще будучи юным учеником, Гаусс сумел отыскать прекрасное среди очевидно простых, но лишенных красоты вычислений.
Субботняя прогулка
Субботняя прогулка, странно выглядящая головоломка, на первый взгляд не имеет ничего общего с математикой, но все же является достойным примером красоты математического мышления. Так как же она звучит?
В субботу в 9 часов утра Арсен пускается в путь по горной тропе к дому Данила. Он остаётся ночевать в доме своего друга, и затем возвращается по той же тропе в 9 часов утра уже в воскресенье. Есть ли точка на горной тропе, по которой Арсен проходит в одно и то же время и воскресенье, и в субботу? Заметьте, что нет никаких предположений относительно скорости Арсена в любой из дней: в субботу он может идти со скоростью 5 км/час, а в воскресенье – 6 км/час, а также Арсен может ускоряться и замедляться в любой из дней, а может даже устроить перевал прямо на тропинке. Мы ничего не знаем о скорости Арсена, что, на удивление, и не имеет значения для решения головоломки!
Решение кроется в нестандартном рассуждении: представьте, что в 9 утра в воскресенье, когда сам Арсен возвращался к себе, навстречу Арсену вышел его брат. А шел он с такой же скоростью и по той же тропинке в точности, как и Арсен в субботу. Очевидно, что в некоторый момент X они встретятся где-то посередине тропинки, а это точка встречи и будет нашим ответом!
Термометры и барометры
Сейчас давайте рассмотрим казалось бы абсурдное и труднодоказуемое утверждение, имеющее довольно необычное и элегантное математическое обоснование. Утверждение гласит:
В любой момент времени на Земле есть две диаметрально противоположные точки (антиподы), в которых значения температуры и давления совпадают.
Даже если это правда, доказать наличие данных точек ужасно трудно, не так ли? Но все же давайте попробуем.
Для начала возьмем два термометра и любые две случайные противоположные точки \(A\) и \(B\) на поверхности Земли, причем точки должны быть с различными показаниями температуры в данный момент времени. Предположим, что температура в точке \(A\) выше, чем в точке \(B\) (то же рассуждение работает если температура в \(B\) выше, чем в \(A\)). Теперь поменяем местами термометры так, чтобы они всегда оставались диаметрально противоположными в любой точке своего пути относительно центра Земли.
В процессе замены обратите внимание, что существует по крайней мере один момент времени, в котором показания температуры обоих термометров равны.
Таким образом, мы доказали, что в любой момент времени на Земле существуют две противоположные точки с одинаковыми температурами.
Что же делать дальше? Повторяя тот же процесс с бесконечным множеством наборов антиподов \(A\) и \(B\), мы получаем целую непрерывную полосу этих антиподов на поверхности Земли с одинаковой температурой. Допустим обратное: нет непрерывной полосы и нет соответственно промежутков. Но тогда это означает, что мы сможем поменять местами термометры \(A\) и \(B\), даже не встретив пересечения, где показания температуры станут одинаковыми, что уже невозможно из доказательства выше.
Теперь возьмем две любые случайные противоположные точки на этой полосе и измерим атмосферное давление в каждой точке с помощью барометра. Начнем плавно менять местами барометры между этими двумя точками, при этом двигаясь исключительно по полосе антиподов с одинаковой температурой (существование такой полосы мы доказали выше). И снова в процессе замены мы встретим по крайней мере один момент времени, где графики давления пересекаются, и именно в этот момент показания давления на обоих барометрах будут одинаковыми.
Поскольку мы уже двигались по изотермической (имеющую одинаковую температуру) полосе на поверхности Земли, эта пара противоположных точек будет иметь одинаковую температуру и давление.
Таким образом, мы показали существование по крайней мере одной пары противоположных точек на Земле, где в определенный момент значения температуры и давления будут соответственно равны друг другу. Что и требовалось доказать!
Это утверждение, являясь частным случаем теорема Борсука–Улама, и казалось бы не имеющее практического применения, стало революционным прорывом в топологии и явным образом доказало, что невозможности в природе становятся возможными если суметь рассуждать «правильно»!
Заключение
Математика – не то, что мы привыкли встречать в школе. Математика – это много больше, чем просто числа, методы и формулы. Может сами методы обычно лишены красоты, но искусство рассуждать математически обязательно включает в себя творчество, воображение, вдохновение и изобретательность.
Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.
Редактор статьи: Дарина Мухамеджанова
