[Математика ғажабы] Шексіздік

Kalmakhanov Arystan

19 дек. 2021 г. • 6 мин. чтения

«Пән ғажабы неде» жобаның барлық мақалалары
«Математика ғажабы» циклдың басқа мақалалары
Визуалды дәлелдемелер
Байес теоремасы
Ойлаудың көркемдігі
Сымдарды кесеміз
Геометриямен жасырынбақ ойнау
Пифагор теоремасы

Баршамызға математиканың өзімізге таныс нақты сандармен қосу, көбейту сынды амалдарды орындағанда қалай жұмыс жасайтындығы таныс. Алайда сандар аяқталып, шексіздікке өткен кезде математикадағы қызық енді басталады.

Математикада шексіздік сіз ойлағанға қарағанда маңыздырақ рөл атқарады. Математиканың көптеген бөлімдерінің маңызды бөлігі бола тұра, кей жағдайларда шексіздік адам сенгісіз, әдемі шешімдерге де әкеле алады.

«Гранд-отель» парадоксы

Көз алдыңызға бөлмелер саны шексіз болатын қонақ үйді елестетіңіз және осы бөлемелердің барлығында тұрғындар қоныстанған екен. Бір кезде осы қонақ үйге тоқтағысы келген тағы да бір қонақ пайда болады. Қалай ойлайсыздар, қонақ үй әкімшілігі не істемек? Таңғаларлық жағдай, бірақ олар оған бас тартпайды! Әкімшілік жай ғана бірінші бөлмедегі қонақты екінші бөлмеге көшуді сұрайды. Ал екіншідегін үшіншіге, үшіншідегін төртіншіге және осылай шексіздікке дейін. Сонда жаңадан келген қонаққа бірінші бөлме босайтын болады.

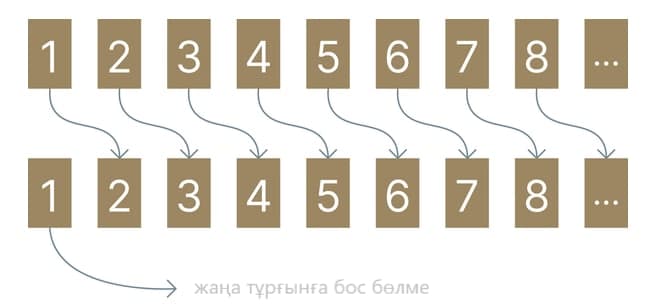
Тамаша шектердің ғажаптылығы

Шындыққа жанасатын басқа бір мысалды қарастырайық. Сіз банкте қандай да бір пайызбен депозит ашқыңыз келді деп елестетейік. Уақыт өте келе алғашқы салған соммаңыз пайыздық мөлшерлемеге сай өсіп отырады. Сіздің ақшаңыз әр ай сайын $10%$-ға өседі деп айталық, онда депозит ашылған кезден бастағанда бір жылдан соң сіздің ақшаңыз $1.1^{12}=3.14$ ($pi$ санына ұқса шама, бірақ бұл тек кездейсоқтық) есе өседі. Депозиттегі есепшоттың мөшерінің уақытқа тәуелді формуласын жазып көрейік. $P(t)$ — депозиттегі ақшаның $t$ ай өткеннен кейінгі мөлшері болсын, ал x бастапқы салым болсын.

$10%$ болған мысалды қолдана отырып, бастапқы сомманы $100$ теңге деп алайық. Осылайша бізде: \[P(0) = 100\\ P(1) = 100 + 100\cdot \frac{1}{10}=100\left(1+\frac{1}{10}\right),\] себебі, бастапқы сомма $10$ пайызға өседі, ал $10%$ — бұл оннан бір бөлігі. Ал енді $P(2)$ есептейміз:\[P(2) = 100\left(1+\frac{1}{10}\right) + 100\left(1+\frac{1}{10}\right)\cdot \frac{1}{10}=\] \[= 100\left(1+\frac{1}{10}\right)\left(1+\frac{1}{10}\right)=\] \[= 100\left(1+\frac{1}{10}\right)^2\]Егер осы операцияны басқа да уақыт аралықтарына қолданатын болсақ, онда біздің функцияның аргументі(салымды ашқан уақыттан бастап есептегендегі өткен айлар саны) жақша ішіндегі өрнектің дәрежесіне сәйкес келетінін байқауға болады, яғни функцияны келесідей түрде жаза аламыз: \[P(t)=x\left(1+\frac{1}{10}\right)^t\]Қазір шартты аздап өзгертейік. Енді салымның мөлшері айына бір рет емес, екі рет және $10%$-ға емес, $5%$-ға өсетін болсын. Бұл жағдайда функция келесі түрге айналады: \[P(t)=x\cdot\left(1 + \frac{1}{20}\right)^{2t}\]Бұл функциядағы $1 + \frac{1}{20}$ әр ай сайын депозитттің $5%$-ға өсіп отырғанын көрсетеді, ал $2t$ депозиттің өсу жиілігі айына екі ретке артты дегенді білдіреді. Осы екі функция арасында айырмашылық бар ма? Мысалыға, сіз досыңызбен депозитке $1000$ теңге салдыңыздар дейік, бірақ досыңыз бірінші функция шартымен, ал сіз екінші функция шартымен депозит аштыңыздар. Арада бес жыл өткен соң кімнің депозитінде ақша көбірек болады? Құттықтаймыз, дәл сіз үлкен пайдаға кенелесіз! Бірақ неліктен солай болады? Бұл көзге біртүрлі болып көрінгенімен, екінші функция біріншіге қарағанда жылдам өседі. Осылайша пайыздық мөлшері аз болғанына қарамастан сіздегі ақша жиірек өсіп отырады да, сәйкесінше депозиттегі ақша да көп болады.

Бір кезде ғалымдар егер депозиттегі ақшаны айына шексіз көп рет және шексіз өте кішкентай пайызбен өсіретін болса, не болады деп ойланған. Өткен мысалдағы логиканы қолдана отырып, біз бұл функцияның келесідей түрдей болатындығын білеміз:\[P(t)=x\cdot \left(1+\frac{1}{n} \right)^{nt}\] Бұл жердегі $n$ дегеніміз айына неше рет өсетінін көрсететін жиілік болып табылады, ал $\frac{1}{n}$ дегеніміз шексіз кішкентай пайызды көрсетеді, себебі бізде $n$ деген шексіздікке ұмтылады. Бірақ бізге сомма қызық емес, бізге сол сомманы бір айда қанша есе өсетіні қызық, сондықтанда біз өрнекті жеңілдетіп жазайық:\[\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n\]

Бұл жазба нені білдіреді? Әр қадамда формуладағы n-нің орнына үлкен санды алмастыратынымызды ғана білдіреді. Ал енді бұл өрнектің мәні нешеге тең екенін іздеп көрейік.

$n$ -нің орнына үлкен сан қоюымыз керек: миллион болсын. Не шығады екен? Егер калькулятормен есептейтін болсақ, онда төмендегідей шығады: \[\left(1+\frac{1}{1000000}\right)^{1000000}=2.71828\]Басқа да үлкен сандарды байқап көріңіз. Уақыт өте келе сіз калькулятордың бір санды қайталай беретінін байқайтын боласыз. Ол Эйлер тұрақтысына жуық мән. Оның нақты мәнін $n$ шексіздік болған кезде ғана анықтай аламыз. Ал енді ойланып көріңізші: қандайда бірден үлкен бір санды шексіз болатын дәрежеге шығарғанда шығатын мән үштен аспайтын болады. Бұл керемет емес пе?

Мұндай шектерді екінші тамаша шектер деп те атайды.

Әзірше оның дәлелдемесін кейінге қалдыра тұрып, бірінші тамаша шекке өтейік: \[\lim_{n \to 0} \frac{\sin(n)}{n}, \quad (\text{$n$ радианмен берілген}) \]

Бұл шекте $n$ шексіз үлкен санның орнына, керісінше шексіз өте кіші, $0$-ге ұмтылатын, бірақ нөлге тең емес санға ие болады.

Бұл шекті өзіңіз дәлелдеуге тырысып көріңіз. Егер де дәлелдемелер шытырманында қалып қойсаңыз, төменде қадам бойынша жазылған осы шектің интутивті дәлелдерінің біріне әкелетін нұсқаулықты көрсетеміз.

$1$. Радиусы $1$, центрі $O$ болатын шеңбер сызыңыз.

$2$. $OA$ және $OB$ болатын $2$ радиусты жүргізіңіз.

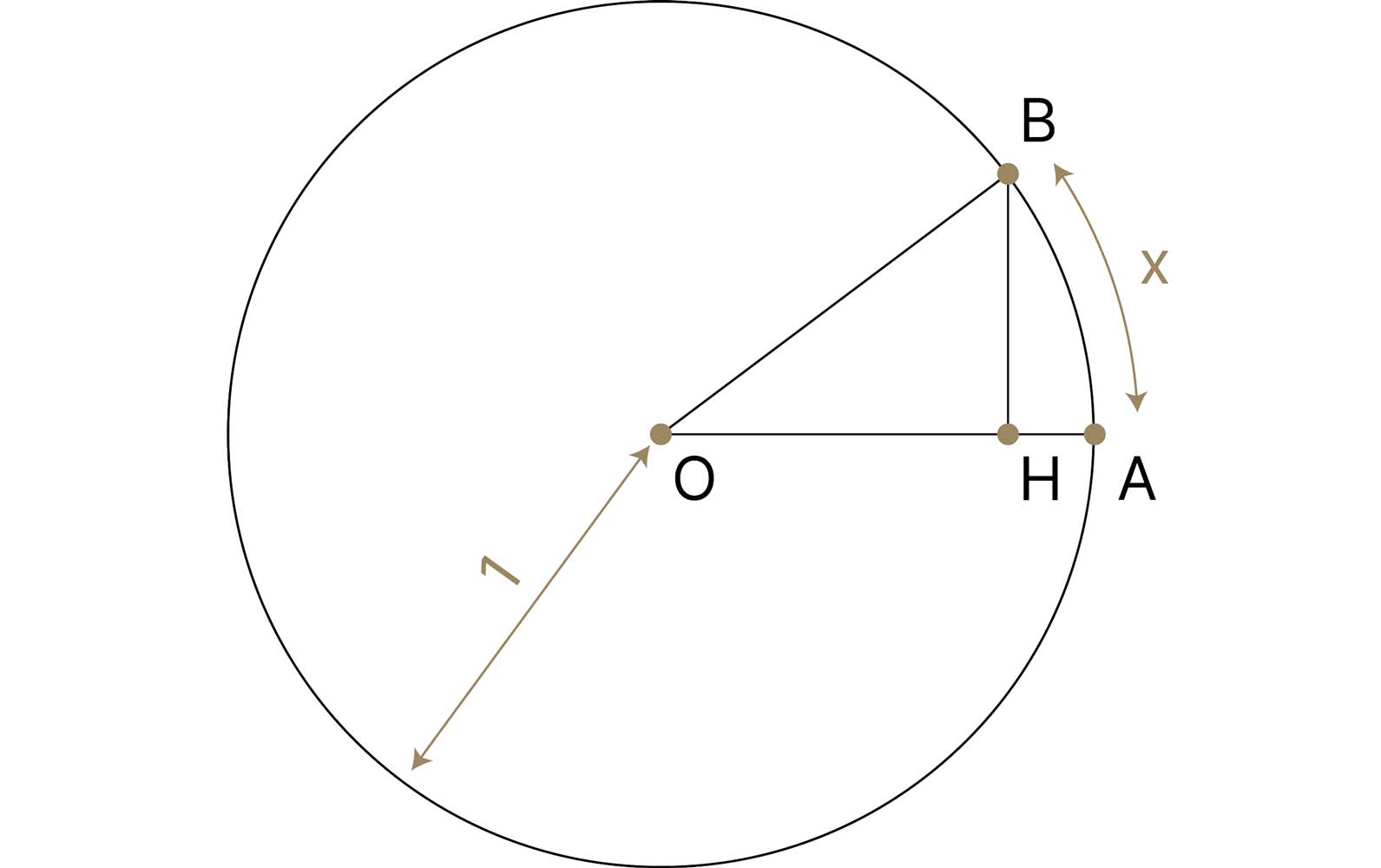
$3$. $AB$ доғасы неге тең? $\angle AOB$ бұрышының синусы ше? Олардың арасында қандай байланыс бар?

$4$. Жоғарыда айтылған сұрақтардың жауабы: егер доғаның ұзындығы $x$ болса, онда $\angle AOB$ бұрышы $x$ радианға тең, ал $\sin (x)$ дегеніміз $B$ нүктесінен $OA$-ға түсірілген биіктікке тең.

$5$. $\angle AOB$ бұрышы кіші болған сайын, доғаның ұзындығы мен биіктігі жақындай беретінін байқаймыз. Осыған сәйкес $x$ пен $\sin (x)$ салыстырылады.

Шексіз сандар қатары туралы парадокс

Кейде шексіздікпен жұмыс жасау бізді әртүрлі парадокстарға әкеледі. Мысал ретінде шексіз сандар қатарының қосындысын алайық:\[1-1+1-1+1-1+1-1+\dots \]Әр жақша нөлді беретіндей етіп жақшаларды орналастырайық:\[(1-1)+(1-1)+(1-1)+(1-1)+\dots\]Егер осы логикаға сүйенетін болсақ, ондай жауап 0 екені айдан анық. Ал осы есепті өзгеше жолмен шығаратын болсақ не болар екен? Тағы да жақшалар қояйық, бірақ бұл жолы басқаша қоямыз. Бірінші қосылғыш жұпсыз қалсын, онда осылай шығады: \[1-(1-1)-(1-1)-(1-1)-\dots\] Бұлай болатын болса, онда бірінші қосылғыш бірге тең, ал қалғандары нөлге тең екені көрініп тұр. Онда соңғы жауаптың мәні $1$ болады.

Осы есепті қайтадан шығарып көрейік, бірақ қосындыны бұл жолы да басқаша жазайық. Екінші қосылғыш біріншінің орнына, үшінші екіншінің орнына, төртінші үшіншінің және осылай жалғаса береді, ал бірінші қосылғыш ең соңында тұрсын (шексіз бөлмелі қонақ үй мысалындағыдай). Жақшаларды қойып, тағы да бірінші санды жұпсыз қалдырсақ, келесідей болады:\[-1+(1-1)+(1-1)+(1-1)+\dots\]Сонда бірінші сан $-1$, ал қалғандары – $0$ болады. Яғни, жалпы қосындысы $-1$-ге тең.

Ал енді барлық қосындыны $S$ деп алып, $1-S$ неге тең екенін тауып көрейік:\[S =1-1+1-1+1-1+1-1+\dots\\ \] \[1-S=1-(1-1+1-1+1-1+\dots)=\\ \] \[=1-1+1-1+1-1+1-1+1-1+\dots\]Сонда $1-S=S$. екені шығады. Таңғаларлық жағдай! $S=0.5$ болып шығатын сызықтық теңдеу секілді.

Сонымен бұл шексіз сандар қосындысы неге әкеледі? $0, 1, −1$ немесе $0.5$ па? Негізінде бұл жауаптардың біреуіде дұрыс емес, себебі мынадай қосындылар тарқалатын деп аталады. Басқаша айтқанда, бұл қосындының соңғы мәнін табу мүмкін емес. Оны табу біздің әртүрлі жауаптарға келуімізге әкеледі. Келесі қатарлардың қайсысында соңғы мән болатынын, ал қайсысы тарқалатын екендігін түсінуге тырысып көріңіз:\[1- \frac{1}{2}+\frac{1}{3} - \frac{1}{4}+\frac{1}{5}- \frac{1}{6}+\dots\\ \] \[1+2+4+8+16+32+64\\ \] \[\frac{1}{2} - \frac{1}{3}+\frac{1}{4} - \frac{1}{5}+\frac{1}{6} - \frac{1}{7}+\dots\]

Шексіздіктерді салыстыру

Сіз бір рет болсын натурал сандар көп пе, әлде бүтін сандар көп пе деп ойланып көрдіңіз бе? Ойға қонымды жауап бұл — бүтін сандар, себебі, бүтін сандар ішінде натурал сандар да бар. Бірақ айтылған әр жиын шексіз екенін ұмытпауымыз керек. Қанекей, натурал сандар деп санауда және нөмірлеу кезінде ($1, 2, 3, 4...$) қолданатын сандарды атайтынымызды есімізге түсіріп алайық. Сондықтан бұл сұраққа жауап беру үшін алдымен басқа сұрақ қойып алу керек: «Біз әрбір бүтін санды нөмірлеп шыға аламыз ба?». Енді соны жасап көрейік. Әрбір теріс сан жұп нөмірге сай келетін болсын, мысалыға, $-1 \rightarrow 2, −2 \rightarrow 4$ және т. с. с. Яғни, $N(x)$ нөмірімен тұрған теріс сан мына формуламен анықталады $N(x) = −2x$. Онда оң сандар және нөл тақ сандар арқылы нөмірленетін болады, мысалы $0 \rightarrow 1, 1 \rightarrow 3, 2 \rightarrow 5$ және т. с. с. Онда $x\geq0$ болған кезде оның формуласы $N(x) = 2x + 1$ болмақ. Сонда әр бүтін санға бір натурал сан бар болып шығады. Бұл факт элементтер санының (қуаттың) тең екендігін дәлелдейді.

Сонда натурал сандар жиынының қуаты мен нақты сандар жиынының қуаты тең деген сөз. Басқаша айтқанда, бүтін сандар жиыны саналады, себебі олардың әрқайсысына натурал санды сәйкестендіре аламыз, ал бұл оларды санауға болатындығын көрсетеді. Бұдан да қызығы рационал сандарды да санауға болатындығы. Оны көру үшін келесі суретке назар аудару жеткілікті:

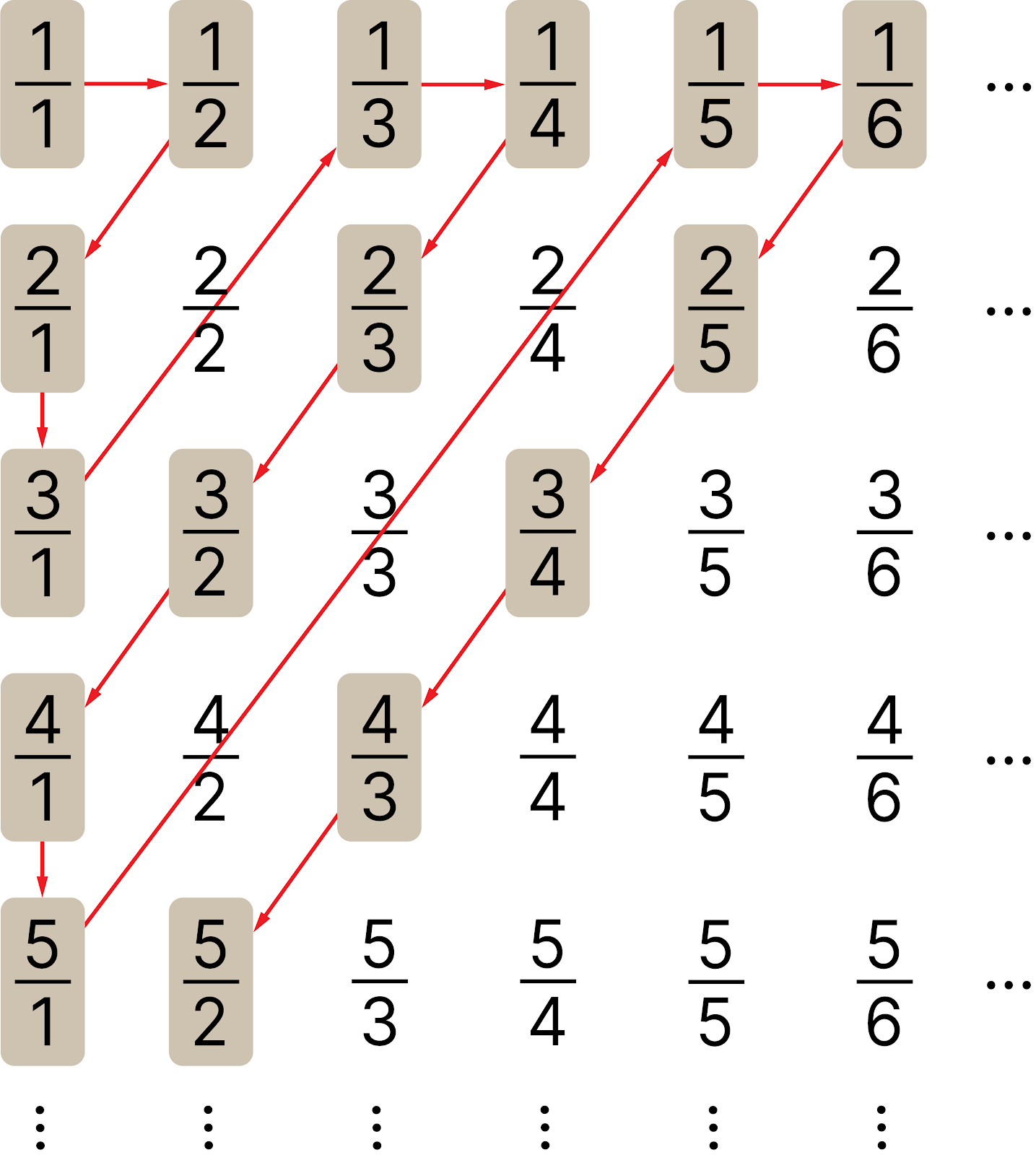
Қызыл көрсеткіш оқтар арқылы барлық рационал сандар бойымен әрбіреуін натурал сандармен нөмірлеп шығуға болатындығы көрініп тұр. Бұл натурал сандар жиыны мен рационал сандар жинының қуаттары тең екендігін көрсетеді.

Жиынның қуатын өлшеу үшін кардиналды сандар қолданылады. Мысалы, натурал сандардың қуаты —$\aleph_0$ (алеф-ноль). Әрбір келесі кардиналды сан алдыңғыға қарағанда үлкен болады. Бұл дегеніміз кейбір шексіздіктер басқа шексіздіктерден үлкен деген сөз.

Математиканың негіздері туралы қарапайым ойлау біздің бұрын қарастырмаған сандардың басқа түрлеріне — кардиналға— әкелді.

Қорытынды

Математикада ол — прима-балерина: басты рөлді сомдайды және бізді мүлдем күтпеген шешімдерге әкелуі мүмкін. Ол көптеген парадокстарды тудыра алады және оларды өзі шешуге бейім. Ол жұмбақ секілді, әрі таңғаларлықтай керемет. Оның аты — шексіздік.

«Beyond Curriculum» қоры «Пән ғажабы неде» циклы материалдарын «Караван знаний» жобасымен серіктестікте және «Шеврон» компаниясының қолдауымен жариялауда. «Караван знаний» – жетекші қазақстандық және халықаралық сарапшылардың қатысуымен орындалған алдыңғы қатарлы білім тәжірибелерін зерттеу мен талқылау бойынша бастама.