[Прелести математики] Режем провода

Все статьи из цикла "В чем прелесть предмета"
Другие статьи из цикла "В чем прелесть математики":
  Визуальные доказательства
  Теорема Байеса
  Красота рассуждений
  Прятки с геометрией
  Бесконечность
  Теорема Пифагора

В один унылый школьный день учитель по робототехнике решил пойти попить чайку, бросив своих нерадивых учеников один на один с, казалось бы, безобидной микросхемой. В микросхеме \(2000\) контактов, и первоначально любые два контакта соединены отдельным проводом. На первый взгляд ничем не примечательная микросхема, но не тут-то было, когда за дело берутся Азамат и Вовка. Да-да, те два закадычных друга, ищущих любую возможность «полакомиться» мозгами своих любимейших учителей, решили сыграть в игру.

Хулиганы по очереди прорезают провода. Начинает Азамат — он за один ход режет один провод, а Вовка, которому нет дела до правосудия, режет либо один, либо три провода за раз. Ученик, отрезающий последний провод от какого-либо контакта, проигрывает, даже если из других контактов все еще выходят провода. Так кто же из них выиграет при правильной, а главное справедливой игре (это когда Вовка держит себя в руках, чтобы не жульничать)?

Да начнется мясорубка!

Жулик Вовка, пообещав не жульничать, решил включить свой мозг на все сто. Кто бы мог подумать, что в его смекалистой голове зреет не простой, а хитрый математический план. Он мысленно разбил все контакты на четыре группы: \(A\), \(B\), \(C\) и \(D\). Как истинный гений, он также мысленно в каждой группе пронумеровал контакты числами от \(1\) до \(500\), запомнив их до конца игры. К сожалению или к счастью, Азамат, в отличие от своего соперника-тунеядца, был обычным пареньком, который просто надеялся на свою интуицию. Вот поэтому без задней мысли Азамат резал свои провода направо и налево…

В это время Вова отвечал на любой ход Азамата так, чтобы для каждого номера \(k\) от контактов \( A_k, B_k, C_k\) и \(D_k\) отходило поровну проводов. До начала игры это условие, очевидно, выполняется (не забывайте, Вовка мог резать один или три провода). Именно благодаря этому условию у нашего жулика Вовки всегда будет возможность ответить на ход бедненького Азаматика. Итак, игра закончилась в пользу Вовки.

С Азамата сошло семь потов, а наш жулик (или все-таки нет?) тихо ухмылялся, пока его одноклассники возбужденно перешептывались, не понимая, как Вовке удалось выиграть… Они не знали его математического плана! И только Бейбарс, тихо сидевший в углу, осознал происходящее, от чего пребывал в большущем удивлении... Судорожно вытерев стекла своих очков, он выбежал из кабинета так быстро, как он только мог. Бейбарс включил кран умывальника уборной комнаты и начал сильно тереть свое лицо водой, пока ужасающие воспоминания пробегали перед его глазами.

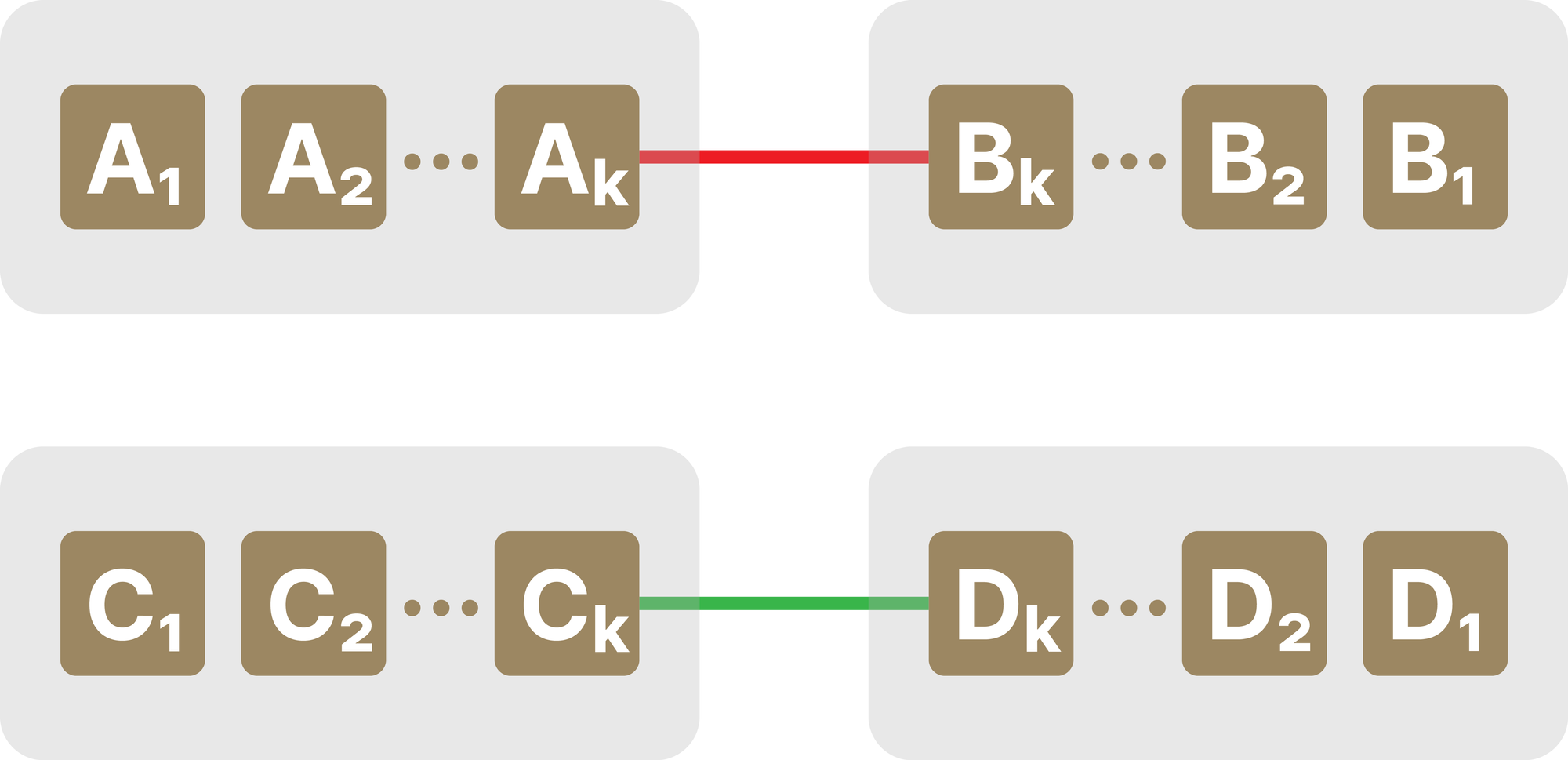
«Если Азамат перерезает провод между контактами одной группы, например, провод \(A_i A_j\), то Вова перережет провода \(B_i B_j\), \(C_i C_j\) и \(D_i D_j\). Если Азамат перерезает провод между контактами из разных групп и с разными номерами, например, провод \(A_i B_j\), то Вова в ответ перережет провода \(A_j B_i\), \(C_i D_j\) и \(C_j D_i\).

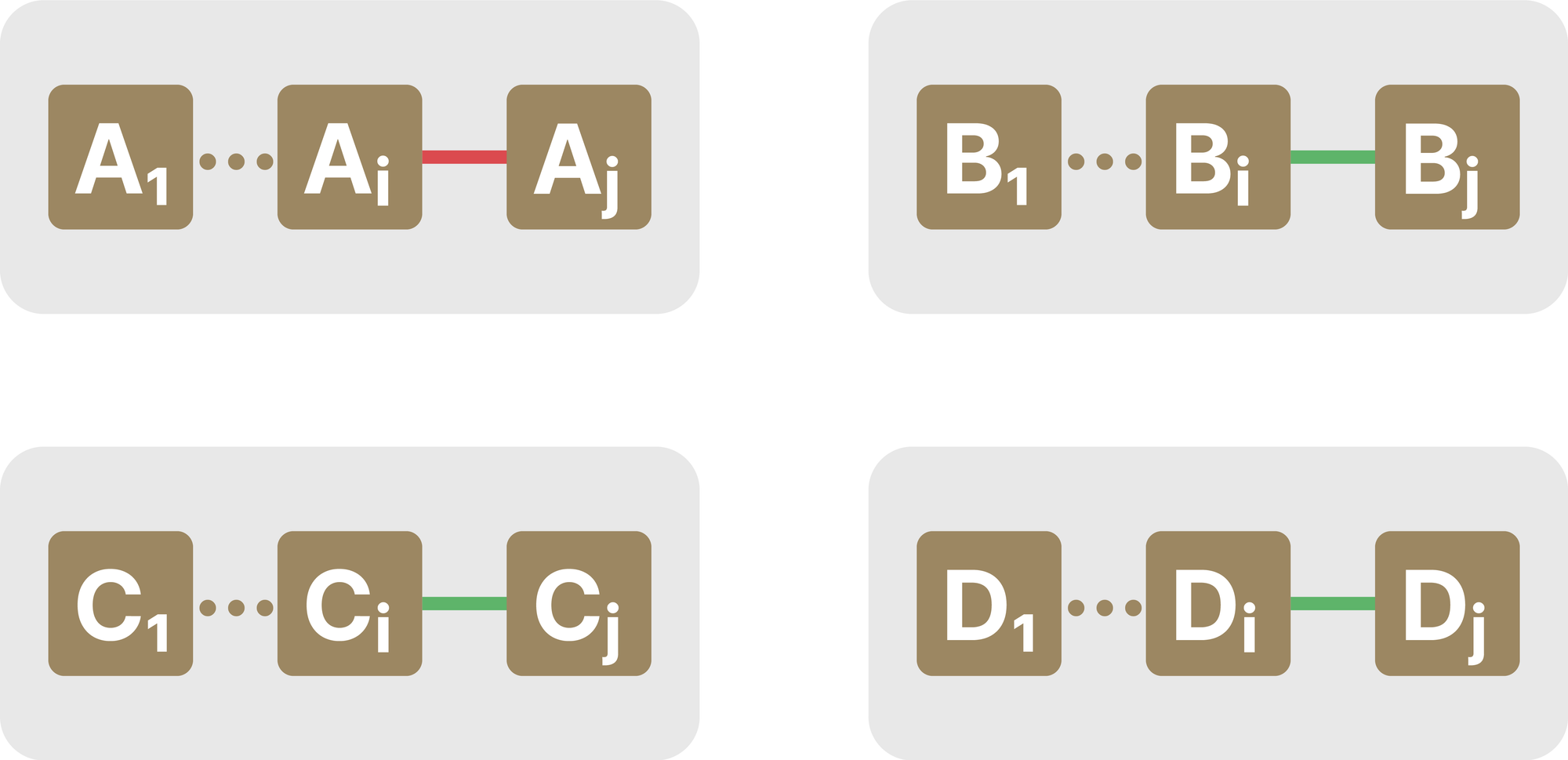
Если же Азамат перерезал провода между контактами из разных групп, но с одинаковыми номерами, например, провод \(A_k B_k\), то Вовка перережет провод \(C_k D_k\)»

Одноклассники Бейбарса крутили своими пальцами у висков, обсуждая его странное поведение. Но они не осознавали, что это была стратегия Вовы, которую их одноклассник Бейбарс так ловко раскусил. Однако оставался единственный вопрос, который все мучил бедного Бейбарса – почему такие ходы вообще возможны?

Бейбарс посмотрел на свое отражение в зеркале, без устали твердя тихое «как». И вдруг он понял:

«Ну конечно! Такие ходы Вова может сделать: из возможности отрезать один провод от некоторого контакта следует возможность отрезать по одному проводу от контактов с таким же номером. Ведь каждый раз после хода Вовы от контактов \(A_k, B_k, C_k\) и \(D_k\) отходит поровну проводов. Иначе говоря, если бы Вова сделал так, чтобы от какого-то контакта не выходили провода, то сделал бы он это только потому, что из контакта такого же номера выходило ноль проводов. Согласно своей стратегии, Вовка решил приравнять количество выходящих проводов, что означает, что до этого Азамат уже отрезал последний провод какого-то контакта. Значит, Вовка всегда сможет сделать ход, и, так как количество проводов конечно, проиграет Азамат, как бы он ни старался...»

Пораженный своим гениальным открытием, Бейбарс не заметил, как позади него скрипнула дверь. Темный силуэт, мелькнувший в отражении зеркала, зловеще прошептал:

«Мы же оба понимаем, что происходит с теми, кто знает лишнее…»

А на этом все!

А кем вы бы хотели стать в этой истории? Учителем по робототехнике, пьющим чай во время урока, или Азаматом – любителем бить баклуши? Одноклассниками, неспособными раскрыть секрет победы Вовки? Или трусливым Бейбарсом, который пусть раскусил Вовку, но испугался уличить его в скрытом жульничестве?

Ну, а если ваш ответ – сумасшедший Вовка, который придумывает гениальные планы, то цикл статей «В чем прелесть предмета» и BeyondCurriculum именно для вас! В нашей подборке по подготовке к олимпиадной математике вы можете найти еще более интересные задачи, которые даже Вовка не сумеет решить!

(Данная задача была взята из Всероссийской Олимпиады по математике \(1999\) года)

Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.

Редактор статьи: Дарина Мухамеджанова