[Прелесть математики] Прятки с геометрией

Все статьи из цикла "В чем прелесть предмета"
Другие статьи из цикла "В чем прелесть математики":
  Визуальные доказательства
  Теорема Байеса
  Красота рассуждений
  Режем провода
  Бесконечность
  Теорема Пифагора

Принято считать, что любую геометрическую задачу можно решить аналитически. Действительно, если у вас достаточно опыта, то вы сможете с легкостью (а может и нет) составить декартовую или барицентрическую систему координат и посчитать всю геометрию «числами».

И это вовсе неудивительно! Чем глубже изучаешь математику, тем быстрее становится понятно насколько непонятны или скорее расплывчаты границы между разными областями самой математики. Тогда возникает вопрос: можно ли решить негеометрические задачи геометрией? И ответ на него:

Да, да, и еще раз да!

Главной чертой геометрии всегда была ее наглядность, что очень помогает в решении любых задач. Геометрический подход к задачам — это мощный «инструмент», который передавался из поколения в поколение. Еще в древние времена, когда не существовало волшебных программ вроде Wolfram Alpha и Photomath, люди объясняли большинство математических операций и свойств объектов с точки зрения геометрии.

Давайте вместе окунемся в представленные ниже примеры негеометрии и попробуем найти в них саму геометрию!

X и Y? Часть 1

Найдите наименьшее значение дроби $\frac{x}{y}, если \sqrt{x-1}+\sqrt{y-1}=1$

Что ж, на первый взгляд, геометрии здесь не наблюдается. Но если я скажу, что данную задачу вы можете решить, начертив геометрические фигуры (нет, не пентаграмму), то это будет чистейшая правда.

Рассмотрим выражение в левой части. Оно имеет смысл только если $x \geq1$ и $y \geq 1$, иначе под корнем будут отрицательные значения. Кроме того, значение каждого из корней не превосходит $1$, что означает — $x \leq 2$ и $y \leq 2$.

Закончив с определением интервала значений $x$ и $y$, давайте мы перейдем к гвоздю всей программы — геометрическому представлению решения уравнения.

Представим график заданного уравнения в декартовой системе координат. Он лежит целиком в квадрате $ABCD$ (см. рис. ниже).

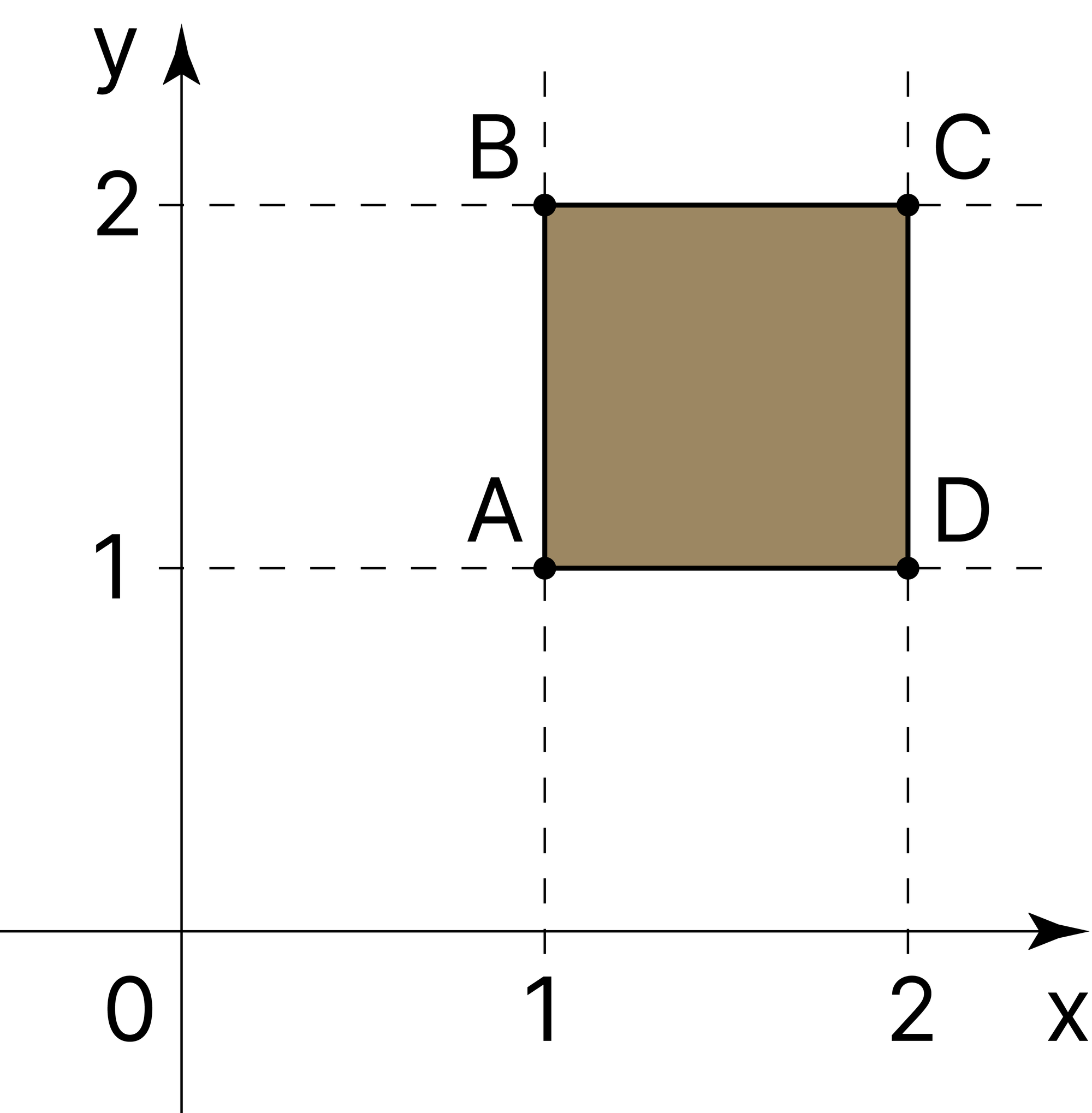
Выражение $\frac{x}{y}$ принимает наименьшее значение только в том случае, когда значение $x$ наименьшее из возможных, а значение $y$ — наибольшее. Из всех точек квадрата $ABCD$ этими условиями удовлетворяет только точка $B(1; 2)$. График заданного уравнения содержит точку $B$, так как при подстановке ее координат в это уравнение получается верное числовое равенство.

Значит ответ равен $\frac{1}{2}$.

X и Y? Часть 2

Разогрелись? Идем дальше!

Найдите наименьшее значение выражения: $|x-y|+\sqrt{(x-3)^{2}+(y+1)^{2}}$

Как вы поняли из предыдущей задачи, когда имеются две неизвестные переменные $x$ и $y$, полезно построить график в декартовой системе координат. И это именно то, что мы собираемся сделать прямо сейчас!

Рассмотрим на координатной плоскости точку $A (3; -1)$ и прямую $y=x$ (см. рис.). Пусть $M(x;y)$, тогда $\sqrt{(x-3)^{2}+(y+1)^{2}} = MA$.

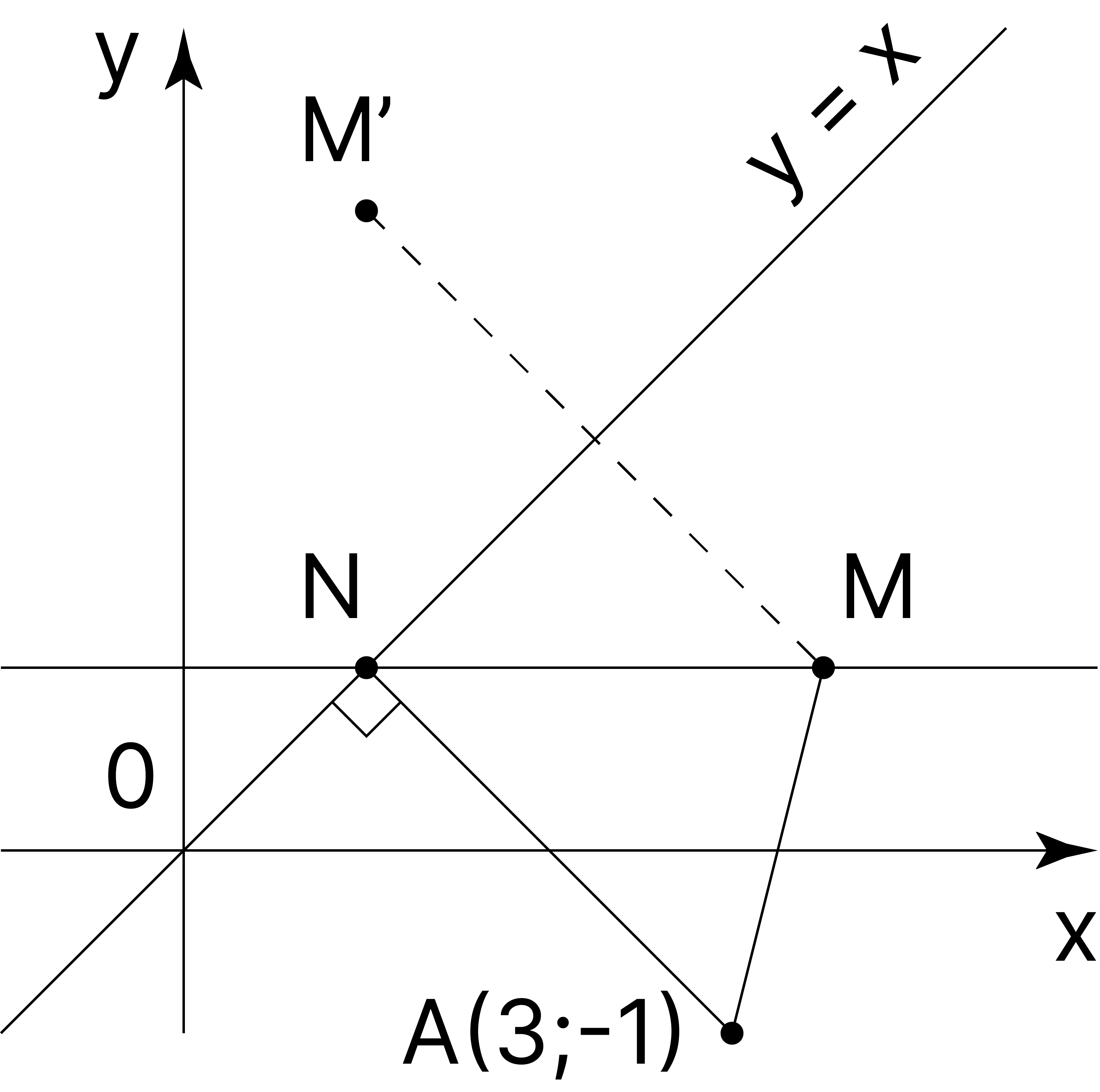
Напомним, что расстояние между точками $A(x;y)$ и $B(m;n)$ на координатной плоскости определяется как $AB = \sqrt{(x-m)^{2}+(y-n)^{2}}$

Заметим, что если точка $M'$ симметрична точке $M$ относительно прямой $y=x$, то $M'(y; x)$. Таким образом, для этих двух точек значение выражения $|x-y|$ одно и то же. Поэтому меньшее расстояние от $А$ будет у той из точек, которая лежит с точкой $A$ в одной полуплоскости относительно прямой $y=x$. Искомая точка $M$ лежит ниже этой прямой, и тогда $|x-y|=MN$, где $N$ — точка пересечения $y=x$ с горизонтальной прямой, проходящей через точку $M$. Значит,по неравенству треугольника $MA+MN \geq AN$, точка $M$ должна лежать на отрезке $AN$, а наименьшее значение длины $AN$ достигается, если $N$ — основание перпендикуляра, опущенного из точки $A$ на прямую $y=x$.

Теперь осталось найти координаты $N.$ Угловой коэффициент прямой $y=x$ равен $1$, поэтому угловой коэффициент прямой $AN$, ей перпендикулярной, равен $-1$, то есть ее уравнение имеет вид $y=-x+с$.

Напомним, что когда две прямые перпендикулярны друг другу, произведение их угловых коэффициентов равно $-1$.

Эта прямая проходит через точку $A (3; 1)$, поэтому $c=2$. Решением системы уравнений $\left. \begin{cases} y=x, \\ y=-x+2 \\ \end{cases} \right.$ является $\left. \begin{cases} x=1, \\ y=1 \\ \end{cases} \right.$, значит прямые $y=x$ и $y=-x+2$ пересекаются в точке $N(1;1)$. Тогда $AN = \sqrt{(1-3)^{2}+(1+1)^{2}} = 2\sqrt{2}$ — это именно то, что нам нужно!

Ответ: $2\sqrt{2}$.

Помогаем бедному Пете

В примерах выше было наглядно показано, как можно решить алгебраические задачи с умело использованной декартовой системой координат. Но не только в таких задачах к нам на помощь может прийти геометрия. Давайте рассмотрим, пожалуй, один из самых неочевидных способов применения геометрического подхода в задаче.

В полдень из Аннино и Ванино вышли навстречу друг другу Аня и Ваня, которые встретились через два часа. В 14:00 из Аннино вышел Петя, который догнал Аню через час, и в этот же момент в Аннино пришел Ваня. На самом деле Петя планировал выйти в полдень и встретиться с Ваней. В какое время произошла бы эта встреча?

В данной задачи нет $x$ и $y$ как в предыдущих, что наводило бы нас на мысль о построении системы координат. Однако легко понять, что в задаче говорится о движении, что так же можно представить в виде графика. Как это было на первых уроках по физике, давайте построим прямоугольную систему координат, показывающую изменение местоположения человека с течением времени.

Изобразим графики движения Ани, Вани и Пети в виде лучей $AD$, $BN$ и $PD$ соответственно как показано на рисунке.

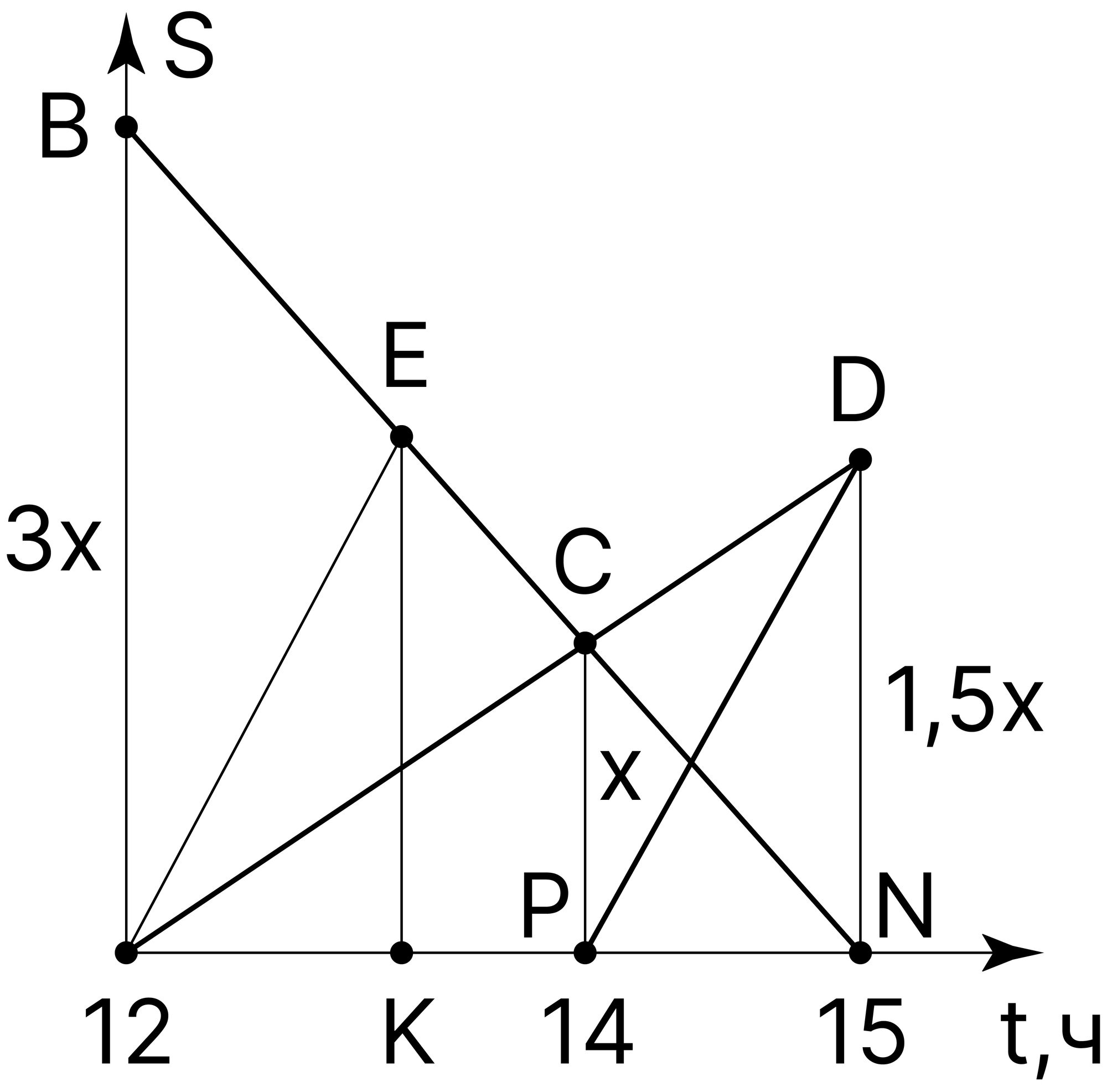
Координаты точек $A$ и $B$ по оси $S$ представляют собой местоположение Аннино и Ванино. Так как Петя так же, как и Аня, вышел из Аннино, его начальная координата по оси $S$ равна нулю. В точке $D$ произошла встреча Ани и Пети, а в точке $C$ — встреча Ани и Вани. Если бы Петя вышел одновременно с Аней, то его место встречи с Ваней была бы точка $E$. Чтобы ответить на вопрос задачи, нам нужно определить координату точки $E$ по оси $t - K$.

Поскольку у Пети всегда постоянная скорость, то график $AE$ планируемого движения Пети будет параллелен $PD$. Так происходит потому, что скорость на данном графике движения определяется как градиент.

Аня и Ваня встретились через два часа после начала их движения,то есть они встретились в 14:00. К нашему счастью, в это же время Петя начал свой путь, что означает, что координата точек $C$ и $P$ по оси $t$ одинакова и равна 14. Кроме того, раз встреча Ани и Пети произошла через час после начала движения Пети, то есть в 15:00, в тот же момент, когда Ваня дошел до Аннино, то координаты точек $D$ и $N$ по оси $t$ аналогичным образом равны. Исходя из этого, мы можем с радостью сказать, что $CP$, $DN$ и ось $S$ параллельны друг другу!

Рассмотрим треугольники $ACP$ и $ADN$. Они обладают общей вершиной $A$ и $CP\parallel DN$, а значит эти треугольники подобны. Тогда если предположим, что $CP = x$, то из подобия будет следовать, что $DN=1.5x$.

Так как ось $S$ и $CP$ параллельны, треугольники $ABN$ и $PCN$ так же подобны, из чего мы получаем, что $AB = 3x$.

Ранее мы говорили, что $AE\parallel PD$. Давайте теперь воспользуемся этим! Они параллельны, а также $EK$ и $DN$ перпендикулярны оси $t$, что означает, что $EK$ и $DN$ параллельны! Следовательно, треугольники $AEK$ и $PDN$ какие? Правильно — подобные!

Пусть $k$ — коэффициент подобия треугольников $AEK$ и $PDN$, тогда $AK = k$, $EK = 1.5kx$. Если мы рассмотрим треугольники $BAN$ и $EKN$, то можно ясно увидеть, что они подобны. Из этого вытекает, что $\frac{1.5kx}{3x} = \frac{3-k}{3}$. Решением этого уравнения является $k = 1.2$. Значит, время планируемой встречи — 13 часов и 12 минут.

X и Y уже не одни

После примеров выше может появиться обманчивое чувство, что в решении негеометрических задач геометрией нужно все время использовать координатную плоскость. На самом деле существует целое множество различных креативных геометрических подходов в решении задач, не требующих системы координат. И на один из примеров мы посмотрим прямо сейчас!

Докажите, что если $0<x<1$, $0<y<1$ и $0<z<1$, то $x(1-y)+y(1-z)+y(1-x)<1$

Рассмотрим куб с ребром $1$. Выберем три ребра, выходящих из одной вершины, и отложим на них отрезки с длинами $x$, $y$ и $z$ (см. рис.).

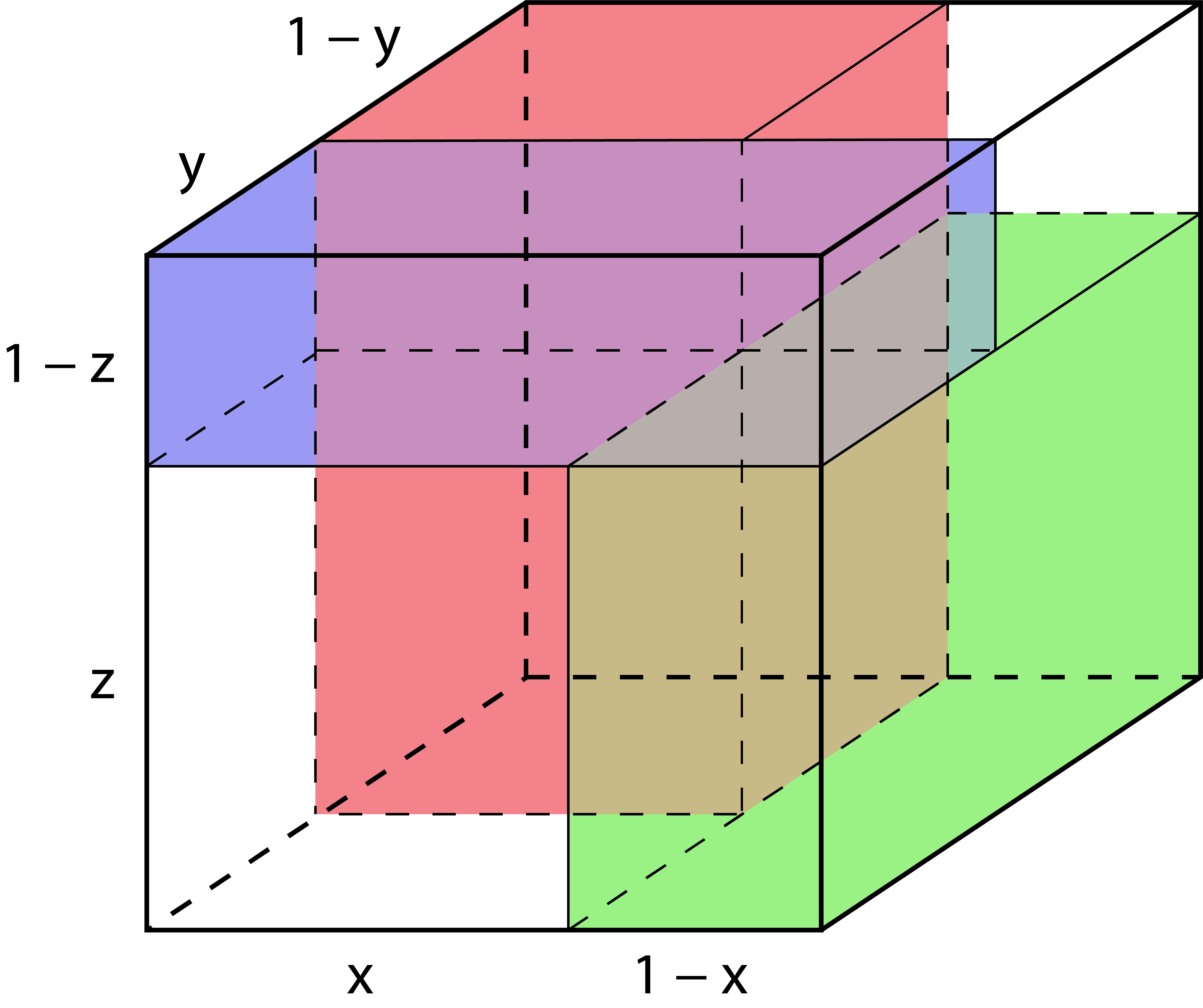
Построим три прямоугольных параллелепипеда с размерами $x \times (1-y) \times 1$, $y \times (1-z) \times 1$ и $z \times (1-x) \times 1$. Так как эти параллелепипеды не имеют общих внутренних точек, то сумма их объемов меньше, чем объем куба, равный 1. Их объемы равны: $x(1-y)$, $y(1-z)$ и $z(1-x)$. Значит, $x(1-y)+y(1-z)+z(1-x)<1$ — что и требовалось доказать.

Получилось очень емкое, простое и несколько забавное решение! Поверьте, вы так же можете решать негеометрические задачи «по-необычному»! Отбросьте предубеждения об отдельно существующих разделах математики. Как бы странно это ни звучало, но математика — это именно то место, где нет никаких законов. Именно здесь вы можете экспериментировать и придумывать свои собственные метода и решения!

Играем в Лондоне!

Геометрия любит прятаться не только в задачах, написанных на бумаге, но и в реальной жизни. Чтобы проверить это, давайте переместимся в дождливый Лондон в Собор Святого Павла.

Шагая по круглой галерее великолепного собора, вы можете изумиться или даже испугаться различных звуков, которые возникли так же неожиданно, как и исчезли в ту же секунду, как только вы отошли на пару шагов. Моэтому это место и называют «Галереей вздохов». Так что именно заставляет вас услышать эти звуки?

Духи? Привидения? Магия вне Хогвартса?

На самом деле всего лишь математика. Тут-то и прячется наша геометрия. Давайте искать!

Я считаю до пяти, не могу до десяти. Раз, два, три, четыре, пять, я иду искать!

Что ж, думаю, вы уже поняли, что этот «шепчущий эффект» связан не с чем иным, как с архитектурой данного здания. Давайте посмотрим на фотографию «Галереи вздохов» Собора Святого Павла,дабы заметить ее главную особенность.

Как вы видите, данное помещение имеет эллиптическую форму. Благодаря такой форме, люди и поверили в магию внутри собора!

Если мы поищем что такое эллипс, то увидим следующее определение:

Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек $F_1$ и $F_2$ равна постоянной величине. Точки $F_1$ и $F_2$ называют фокусами эллипса.

Из определения эллипса следует его оптическое свойство: прямые, соединяющие любую его точку с фокусами, составляют с касательной к эллипсу в этой точке равные углы. Кроме того, из физики вам должно быть известно, что акустические волны распространяются подобно световым лучам — выходя из одного фокуса эллипса, где сосредоточен источник звука, волны собираются в другом его фокусе благодаря отражению об эллипс.

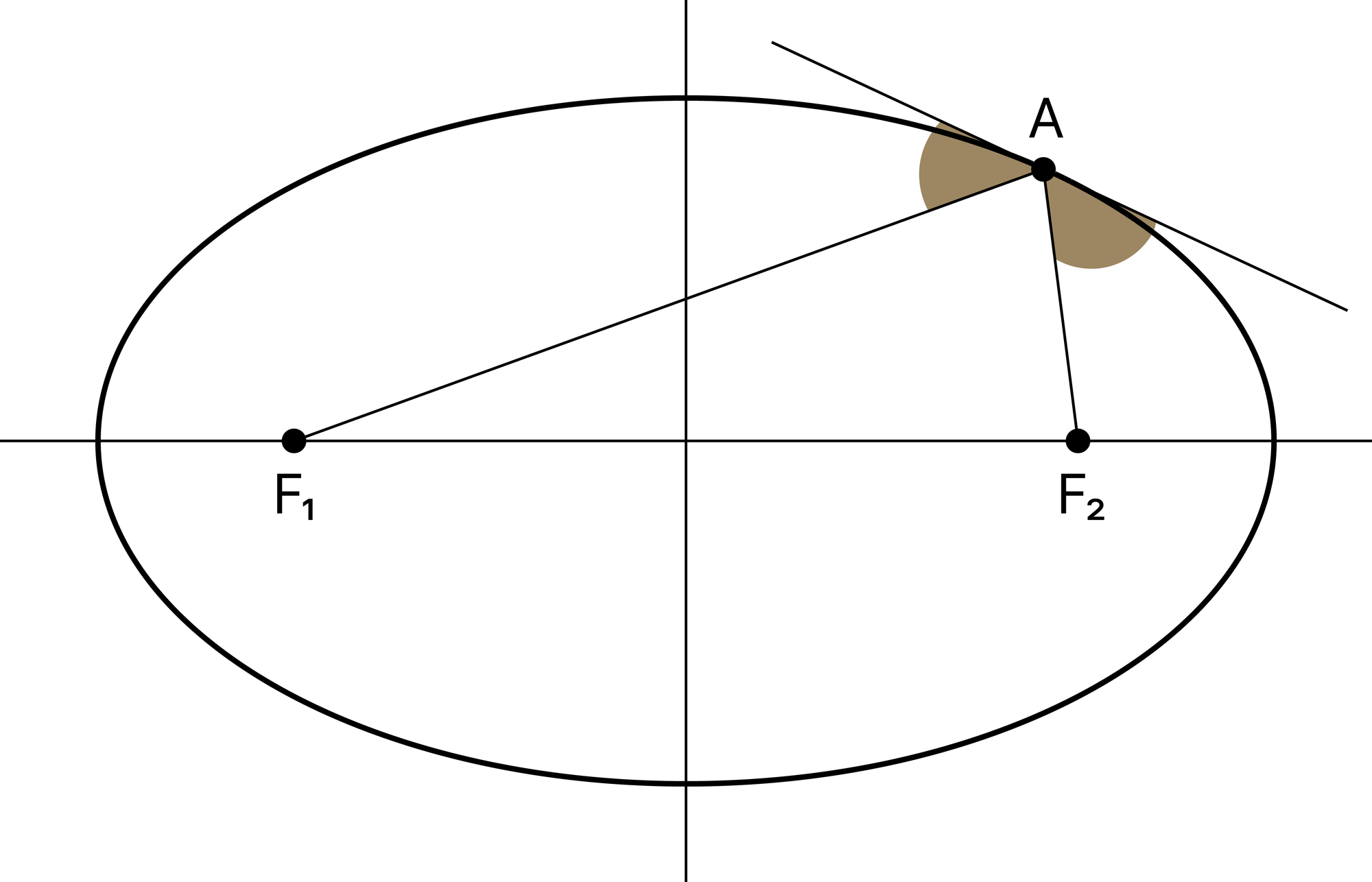
Таким образом, в помещениях эллиптической формы, слова, произнесенные шёпотом в одном из фокусов эллипса, будут услышаны только в другом фокусе, а не во всем помещении, причем шёпот будет услышан, даже если расстояние между фокусами весьма существенно.

Вот так мы опять раскусили геометрию, а также узнали как можно незаметно секретничать с другими людьми в зданиях эллиптической формы. Так что смело начинайте планировать будущий дом в форме эллипса, чтобы разыгрывать своих друзей!

Заключение

Многие недооценивают силу геометрии, считая, что она не особо может пригодиться в жизни. Но правда в том, что геометрия — кроткий раздел математики, полюбивший прятаться. Поэтому, чтобы понять всю суть геометрии, вам придется находиться в постоянных поисках. Эти поиски могут быть долгими и даже мучительными. Однако прелестью игры в прятки с геометрией является не сам ответ на задачу, а процесс поисков, наполненный захватывающими приключениями, и преградами, которые вы, конечно же, сможете преодолеть!

Использованная литература и веб-ресурсы:
А. Д. Блинков “Геометрия в негеометрических задач”
Википедия (https://ru.wikipedia.org/wiki/Шепчущая_галерея)

Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.

Редактор статьи: Дарина Мухамеджанова