[Прелесть математики] Теорема Пифагора

Все статьи из цикла "В чем прелесть предмета"
Другие статьи из цикла "В чем прелесть математики":
  Визуальные доказательства
  Теорема Байеса
  Красота рассуждений
  Режем провода
  Прятки с геометрией
  Бесконечность

Математика не только формулы. Математика – это все, что нас окружает. В ней важно не только знать теоремы и аксиомы, но и понимать, чувствовать ее фундаментальные принципы. К одному из таких фундаментальных знаний можно отнести теорему Пифагора, с которой мы знакомимся еще в школе на уроках геометрии. Однако, как порой это бывает, учебная программа упускает красоту и изящество самой теоремы, чья роль намного важнее, чем нахождение сторон треугольника; теорема Пифагора находит неисчисляемое множество применений в науке и технике – невозможно переоценить ее значимость.

В этой статье мы познакомимся с историей теоремы Пифагора, узнаем, как чертили прямые углы в Древнем Египте, что такое пифагоровы тройки и какой магией обладает математика, спрятанная в простой теореме о сумме квадратов катетов.

История теоремы Пифагора

Теорема Пифагора:

В любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. \[c^2=a^2+b^2 \]

Несмотря на то, что сейчас имя Пифагора навсегда связано с теоремой о квадратах катетов и гипотенузы, мы не имеем никаких сохранившихся письменных свидетельств того, что сам Пифагор открыл и доказал эту теорему. И хотя некоторые авторы античных времен в лице Плутарха и Цицерона считали, что теорему вывел именно Пифагор, первооткрывателем его не назовешь. Что мы знаем наверняка – теорема принадлежит древнейшему периоду пифагорейской математики между VI веком до н. э. и V веком н. э.

Одна скромная глиняная дощечка, найденная археологами XX века в Месопотамии, также выступает против первенства древнегреческого математика. Она наглядно показывает, что теорема могла быть открыта вавилонскими математиками за \(1000\) лет до рождения самого Пифагора.

Эта глиняная табличка, известная как Plimpton 322, датируется примерно XIX-XVI веком до нашей эры. На ней перечислены пятнадцать троек с длинами отрезков, образующих прямоугольный треугольник: \((3, 4, 5)\), \((28, 45, 53)\) и \(65, 72, 97)\), но не \((5, 12, 13)\) или \((8, 15, 17)\), хотя присутствует даже тройка \((12 709, 13 500, 18 541)\)! Получить подобные тройки простым подбором практически невозможно, поэтому ученые предполагают, что автор дощечки знал, как получить больше подобных троек из формулы Пифагора, которая была открыта спустя 1000 лет. Кроме того, Plimpton 322 была написана в том же формате, что и другие административные (не математические) документы того периода. Упоминание пифагоровых троек в подобном “общественном” документе показывает, что теорема Пифагора не являлась математическим открытием для жителей Междуречья, а активно применялась в жизни вавилонян.

На сегодняшний день известно, что задачи и факты, связанные теоремой Пифагора, встречаются и в древнеиндийском трактате VII–V вв. до н.э. «Сульва Сутра», и древнекитайском сочинении «Чжоу-би Суань Цзинь» III–I вв. до н. э., а также в египетских источниках времен фараона Аменемхета I (2300 г. до н.э). Удивительно, как теорема Пифагора занимала умы математиков с древнейших времен. Чего же стоят около 370 разнообразных доказательств, существующих в наши дни!

Доказательство теоремы

В количестве доказательств с теоремой Пифагора не может соревноваться ни одно из существующих математических утверждений. Первоначально, в 1927 году, все эти доказательства были собраны в одну большую книгу по математике и включали доказательство 12-летнего Альберта Эйнштейна, который воспользуется этой теоремой два десятилетия спустя для теории относительности, доказательства Леонардо да Винчи и двадцатого президента США Джеймса Абрам Гарфилда.

С одним из самых простых и красивых доказательств известной теоремы вы могли познакомиться в статье Визуальные доказательства из цикла “В чем прелесть математики”. Здесь же мы представим алгебраическое доказательство этой теоремы, используя один и тот же рисунок.

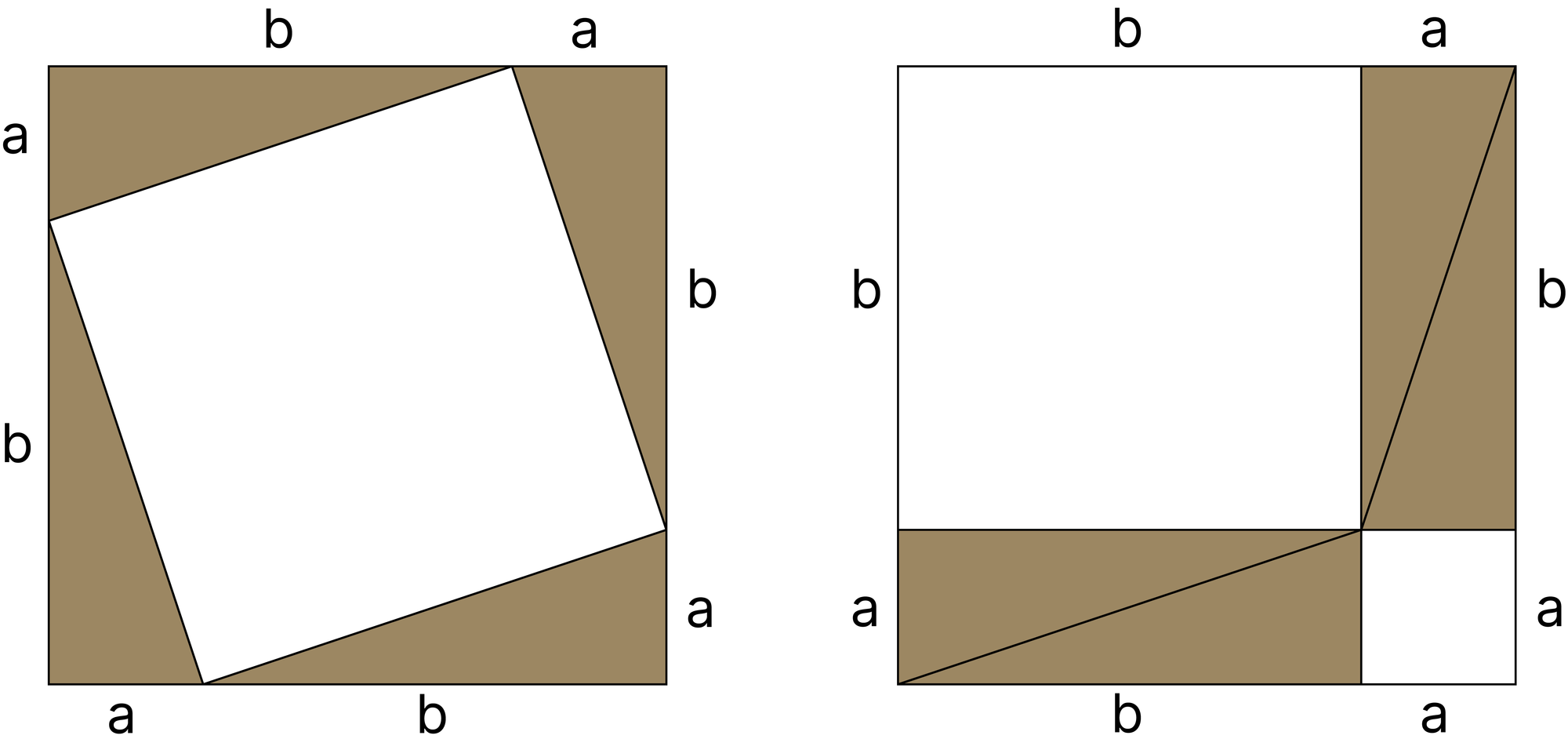
Нарисуем квадрат со стороной \(a+b\), а внутри – \(4\) прямоугольных треугольника с катетами \(a\), \(b\) и гипотенузой \(c\), расположенных так, как изображено на рисунке слева. Давайте посмотрим на площадь большого квадрата с разных точек зрения: с одной стороны, она равна \( (a+b)^2 \), а с другой, сумме площадей этих пяти частей. Площадь белого квадрата равна \( c^2 \), а каждая из четырех серых прямоугольных треугольников по \( \frac{a \cdot b}{2} \). Тогда \[c^2+4 \cdot\frac{a \cdot b}{2} = (a+b)^2 =a^2+b^2 + 2ab.\] \[c^2+ 2ab = (a+b)^2 =a^2+b^2 + 2ab.\] Таким образом, \[c^2=a^2+b^2.\] Теорема доказана!

Теорема работает и в обратную сторону: если для сторон треугольников выполняется известное \(a^2+b^2 = c^2\), то это непременно прямоугольный треугольник!

Пифагоровы тройки

Как начертить прямой угол? Сейчас ответ на этот вопрос кажется предельно очевидным: либо с помощью транспортира и линейки, либо достаточно тетради в клетку. А что делать строителю из Древнего Египта, не знающему ни о тетрадях, ни о транспортире? Он несомненно использовал бы теорему Пифагора (хотя и не называл бы ее именно так).

Чтобы начертить прямые углы, древние египтяне использовали треугольник \(3-4-5\), который по теореме Пифагора является прямоугольным. Сначала они брали веревку и делали на ней отметки, разбивающие веревку на \(12\) \((3+4+5=12)\) равных частей, затем концы веревки связывались. После этого веревку растягивали в виде треугольника со сторонами \(3-4-5\). Получившийся угол между сторонами \(3\) и \(4\) оказывался прямым – то, что надо! Впоследствии именно этот треугольник со сторонами \(3-4-5\) был назван египетским треугольником – в честь своих первых пользователей.

Однако прямые углы можно чертить с помощью не только египетского, но и любого прямоугольного треугольника, чьи стороны удовлетворяют теореме Пифагора. Если стороны такого треугольника являются целыми числами, то их называют пифагоровыми тройками. Представим несколько таких троек:\[3^2+4^2=5^2, 5^2+12^2=13^2, \] \[8^2+15^2=17^2, \, 9^2+12^2=15^2\]Вы наверняка встречали их в жизни, особенно на контрольных по математике, когда учителя стараются составлять задачи с удобными целочисленными ответами.

Любопытно, что все пифагоровы тройки похожи друг на друга как братья. Давайте посмотрим, как получаются Пифагоровы тройки из одноименной теоремы. Вернемся к нашему уравнению и возьмем некую пифагорову тройку \(a,b,c\):\[c^2=a^2+b^2\]А теперь рассмотрим точно такой же треугольник, но со сторонами в два раза больше\(2a,2b,2c\). Тогда получим:\[(2c)^2=(2a)^2+(2b)^2 \Rightarrow 4c^2=4a^2+4b^2 \Rightarrow c^2 = a^2+b^2.\]Выходит, что эта бóльшая тройка, получившаяся из предыдущей поменьше, так же будет пифагоровой. Например, линейные величины треугольника \(6-8-10\) в \(2\) раза больше, чем у египетского треугольника \(3-4-5\). Умножив стороны на любое другое число, мы получим другие значения, которые образуют новые пифагоровы тройки. Так, треугольник \(9-12-15\) получается при увеличении египетского в \(3\) раза, а \(150-200-250\) – при увеличении в \(50\) раз. Такие тройки называются подобными, потому что они не отличаются по своим свойствам, за исключением масштаба, а исходная тройка, являющаяся основой для ряда пифагоровых троек, называется примитивной.

Обобщения теоремы Пифагора

В теоремах часто есть ограничения или условия, в рамках которых известная математикам формула будет выполняться. Сама теорема Пифагора верна только для прямоугольных треугольников и работает только на плоскости, то есть в двухмерном пространстве. А можно ли обойти эти условия? Как придумать более общие теоремы? На самом деле, эти вопросы являются основной заботой многих математиков-исследователей на протяжении столетий, ведь каждый раз нам приходится разрешать все новые ограничения. Чтобы помочь математикам вписать теоремы и формулы в новые отдаленные от конкретного примера условия, на помощь приходит один из методов математического творчества – обобщение. Так, у теоремы Пифагора, выполняющейся строго в прямоугольных треугольниках на плоскости, есть по крайней мере \(2\) обобщения.

Теорема косинусов

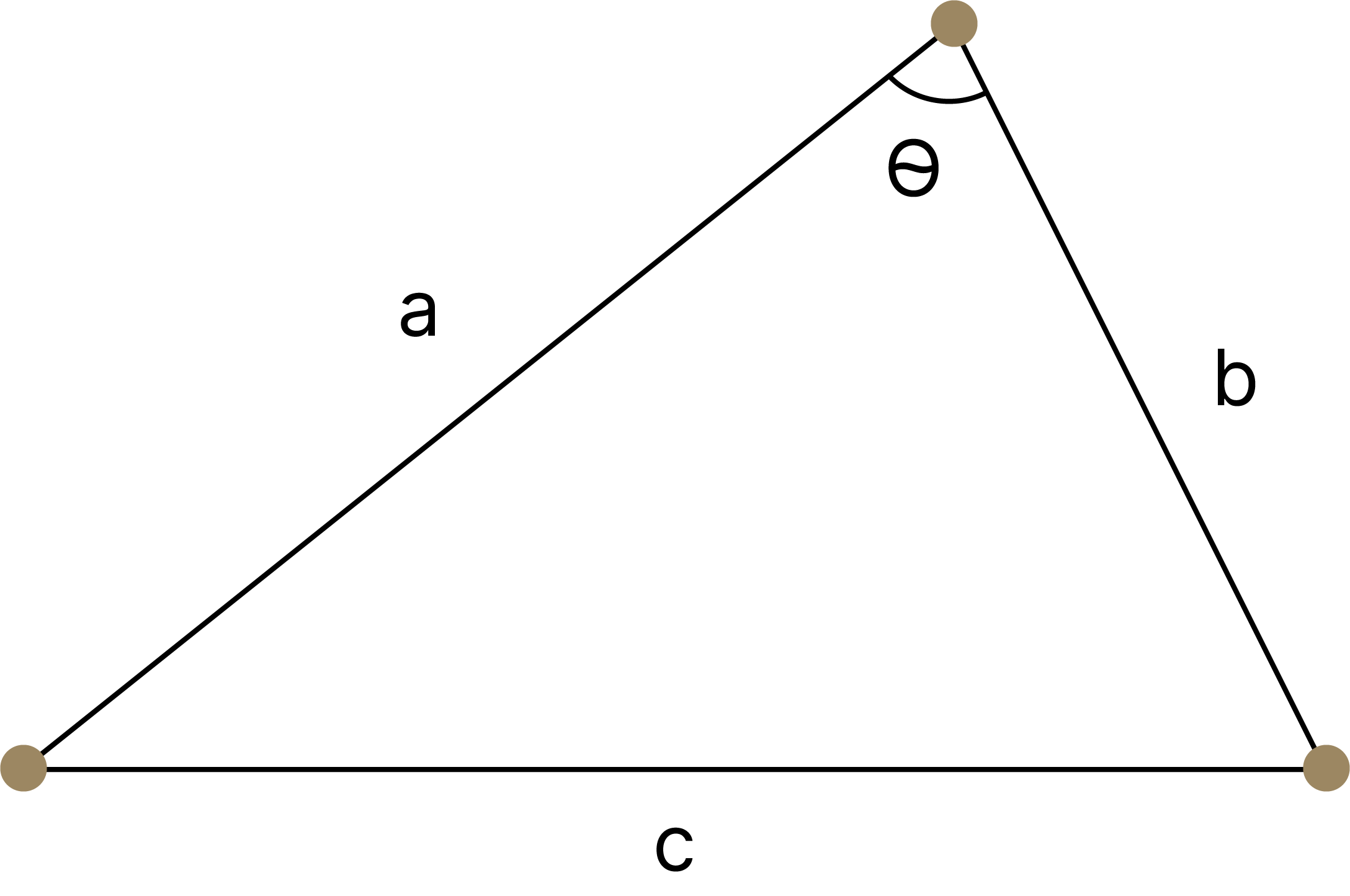
Первым естественным шагом при обобщении теоремы Пифагора является получение утверждения не только для прямоугольных треугольников, но и для всех других – тупоугольных и остроугольных. Как можно выразить одну сторону треугольника, когда мы знаем два другие стороны и угол между ними? Поможет теорема косинусов!

Мы можем выразить сторону \(c\), имея стороны \( a, b\) и угол \( \theta \) между ними, получив уравнение вида: \[c^2= a^ 2 +b^2 - 2ab \cdot \cos{ \theta} \]

Действительно, для прямоугольного треугольника, в котором угол \( \theta = 90^{\circ}\), это утверждение приводит к теореме Пифагора, так как \(\cos{(90^{\circ})} = 0\), а значит \[c^2= a^ 2 +b^2 - 2ab \cdot \cos{90^{\circ} } = a^ 2 +b^2 - 2ab \cdot 0 = a^ 2 +b^2  \]

Диагональ параллелепипеда

Когда прямоугольник расположен на плоскости, легко понять, как использовать теорему Пифагора, чтобы найти длину его диагонали: нужно провести диагональ, делящую прямоугольник на два равных прямоугольных треугольника, и затем найти длину диагонали (гипотенузу) по теореме Пифагора. Это обобщение действует в двухмерном пространстве. А можно ли перейти в наше трехмерное пространство?

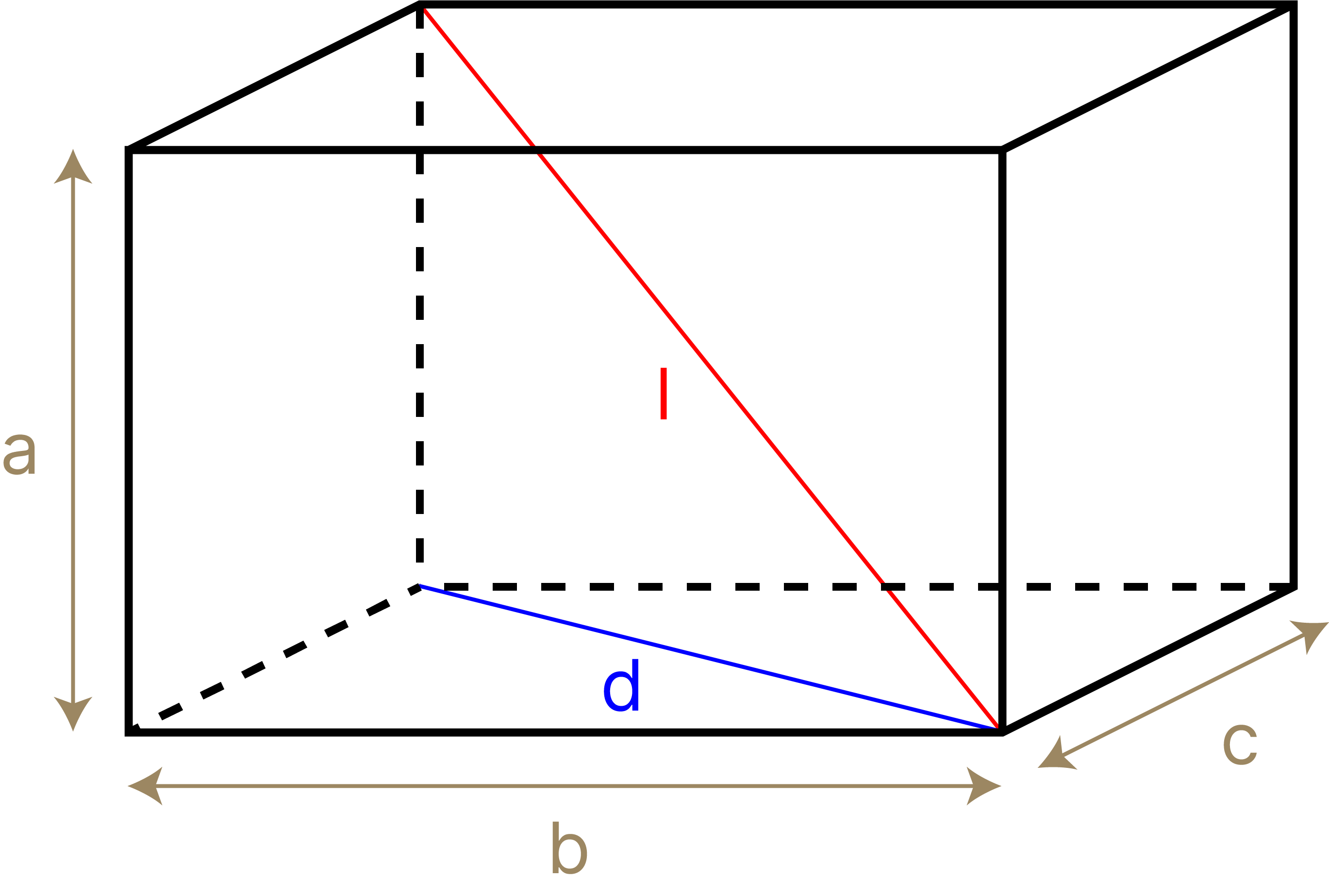
Возьмем диагональ параллелепипеда. Как можно найти ее длину? Оказывается, теорема Пифагора помогает и тут: чтобы найти диагональ, нам достаточно применить теорему два раза. Искомая диагональ параллелепипеда – красный отрезок, представленный на рисунке. Обозначим его длину как \(l\), а длину синего отрезка как \(d\). Можно заметить, что синий отрезок – это диагональ обычного прямоугольника в основании, у которого длины сторон равны \(a\) и \(c\). По теореме Пифагора мы получаем: \[d^2 = a ^ 2 + c ^ 2 \] Теперь же мы можем рассмотреть треугольник, для которого красная диагональ является гипотенузой, а стороны – катетами \(d\) и \(b\). Тогда по теореме Пифагора мы получаем: \[ l^2 = d ^ 2 + b^2\] Вспомнив первое уравнение, полученное из треугольника в основании, мы можем переписать выражение как \[ l^2 = d ^ 2 + b^2 = a ^ 2 + b ^ 2 + c ^ 2.\] В итоге получается сумма трех квадратов, что является теоремой Пифагора для трехмерного пространства.

Любопытно, что теорему Пифагора можно обобщить даже для \(n-\)мерного пространства, где получится сумма \(n\) – квадратов.\[d^2 = d^2_1 + d^2_2 + d^2_3 + \cdots + d^2_n\]

Теорема в реальной жизни

Строительство

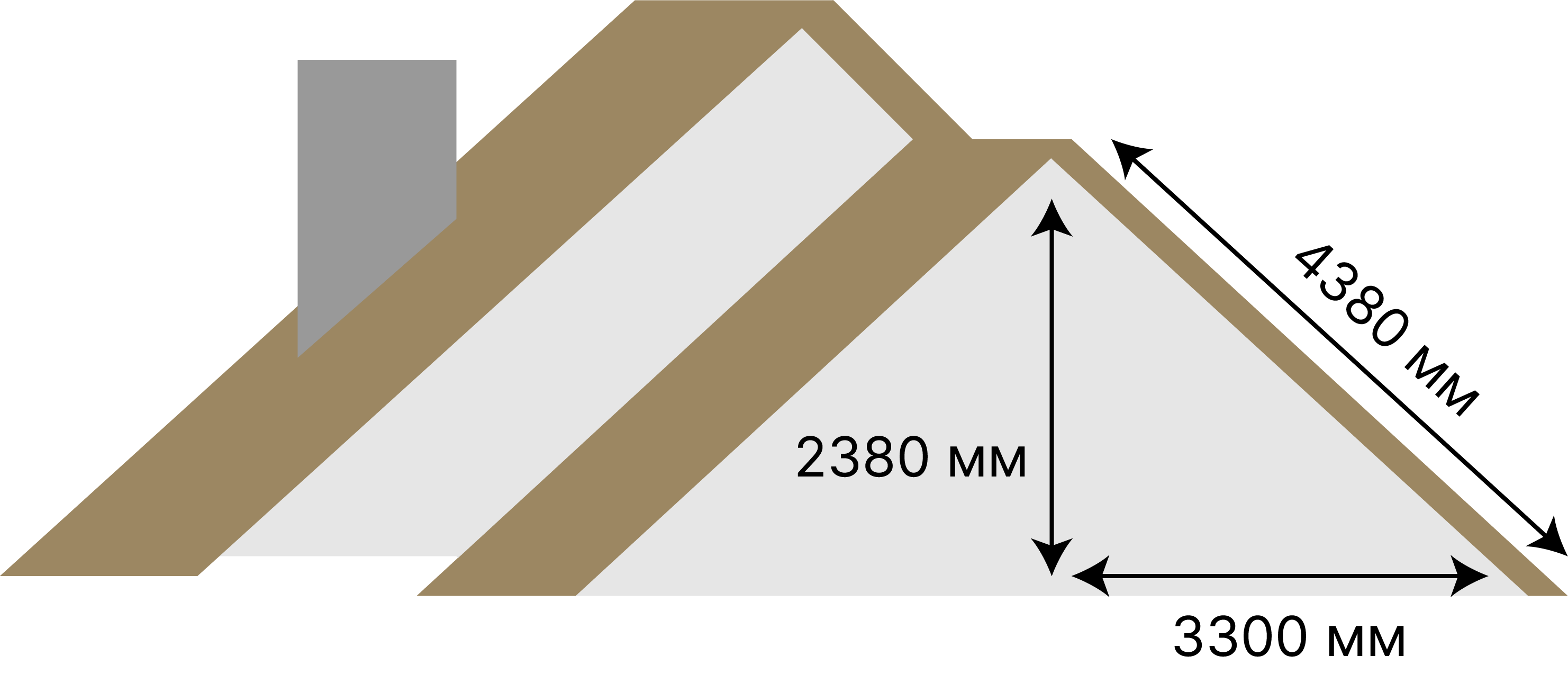
При известных сторонах прямоугольника, теорема Пифагора позволяет найти длину диагонали. Это применение теоремы часто используется в строительстве, деревообработке или других архитектурных проектах. Рассмотрим один маленький пример: предположим, что вам надо построить двухскатную крышу на уже построенное здание (см. изображение ниже). Если вам известна высота и ширина крыши, которую нужно покрыть, вы можете использовать теорему Пифагора, чтобы найти длину крыши. Например, если высота крыши была бы \(2880\) миллиметров, а ширина \(3300\) миллиметров, то по теореме Пифагора: \[c^2=a^2+b^2 =19184400 =  4380^2\] Значит длина крыши должна быть \(4380\) миллиметров, что можно использовать для покупки необходимого количества строительных материалов.

Короткий путь

Множество приключений начинается с небезызвестной фразы “Я знаю короткий путь”. Но кто же знал, что теорема Пифагора вдруг может положить конец этим внезапным путаницам, когда короткий путь оказывается куда длиннее. Представим: чтобы попасть домой у вас есть готовый маршрут – сначала \(120\) метров на юг, а затем \(50\) метров на запад. Общее расстояние, пройденное по этому маршруту, составит \(170\) метров. Другой способ добраться к дому – пойти на юго-запад по третьей стороне треугольника. Если применить теорему Пифагора для вычисления расстояния, получится: \[ 120^2 + 50^2 = 14400 + 2500 = 16900 = c^2 \Rightarrow c = \sqrt{250000} = 130.\] Тогда прогулка по гипотенузе этого треугольного маршрута будет на \(170-130 = 40\) метров короче, чем прогулка по катетам.

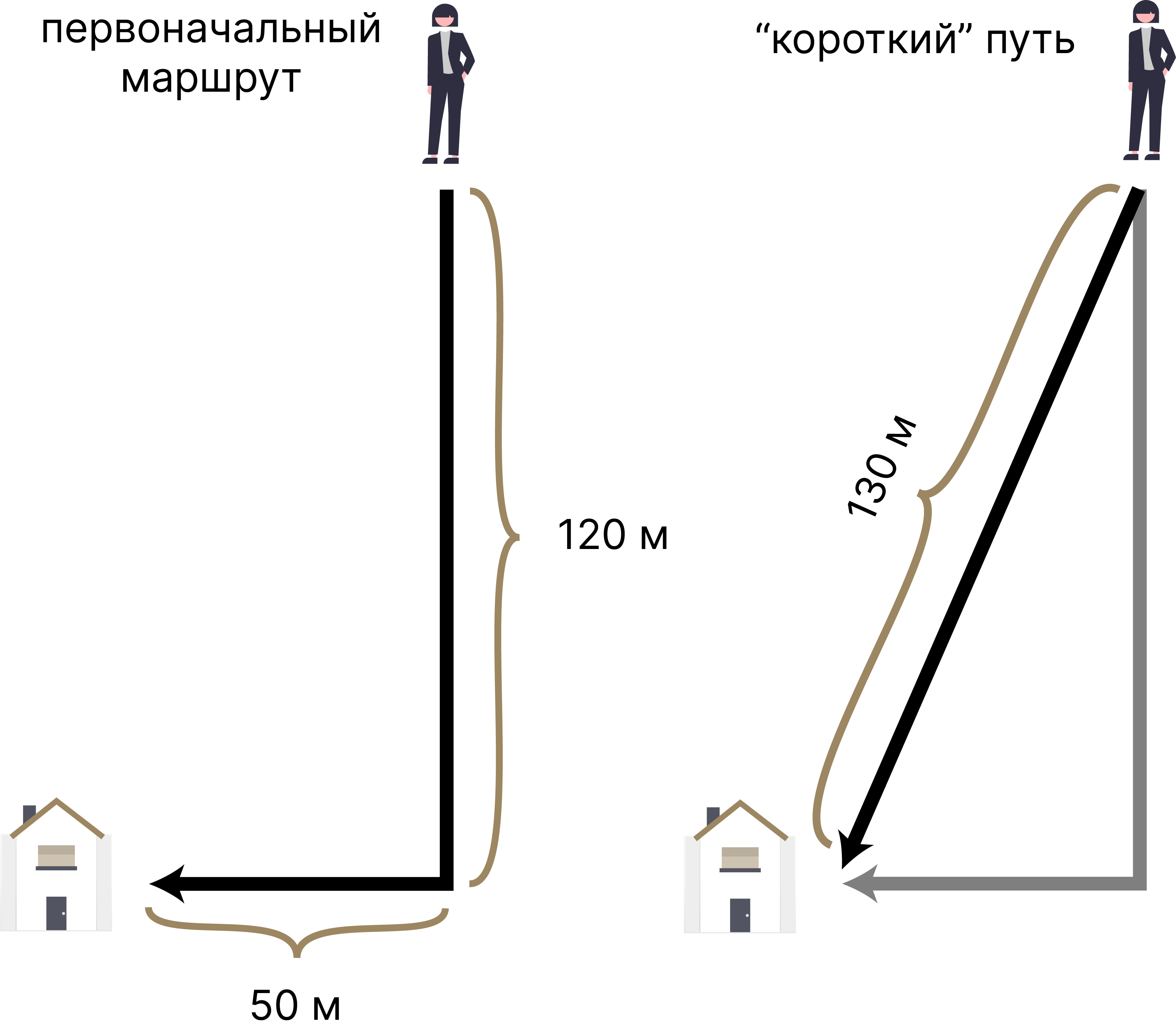
Подобные расчеты будут верны для всех треугольников (вспомните неравенство треугольника), даже не прямоугольных, однако именно в случае прямоугольных треугольников благодаря теореме Пифагора мы можем легко вычислить путь и время, которое можно сэкономить.

Социальные сети

С помощью теоремы Пифагора мы можем разделить любую гипотенузу \(c^2\) на два меньших катета \(a^2 + b^2\). В действительности «гипотенуза» может быть чем угодно: длиной, энергией, работой, отрезком времени или даже количеством людей в социальной сети.

Чтобы увидеть теорему Пифагора в социальных сетях, для начала разберемся что значит “ценность сети” для каждого индивидуального пользователя: чем больше пользователей находятся в какой-то социальной сети, тем полезнее считается сеть для каждого участника. Эта ценность прямо зависит от количества пользователей, ведь подключение нового пользователя означает возможность связаться с большим количеством людей. Роберт Меткалф, со-изобретатель сети Ethernet, сформулировал более формальный закон о математических единицах ценности сети, который затем переименовали в его честь. Закон Меткалфа гласит:

Математическая единица полезности сети пропорциональна квадрату численности пользователей этой сети.

Согласно этому закону, сеть из \(50\) миллионов человек равноценна сумме социальных сетей из \(40\) и \(30\) миллионов человек. Ничего не напоминает? Египетский треугольник со сторонами \(3-4-5\) – примитивная пифагорова тройка. Довольно удивительно: во \(2\)-й и \(3\)-й социальных сетях всего насчитывается \(70\) миллионов человек, но эти сети не являются единым целым. Следовательно, сеть из \(50\) миллионов человек оказывается столь же ценна, как две другие сети вместе взятые.

Так теорема Пифагора разбирается в запутанных социальных сетях и их ценности.

Сортируем книги

Книги в библиотеке или книжных магазинах, как правило, расставляются в алфавитном порядке. И каждый раз, когда библиотека или магазин получают новую партию книг, им необходимо отсортировать эти книги и расставить их в правильном порядке от А до Я. Существует огромное множество способов с разным числом промежуточных операций, с помощью которых можно отсортировать книги. Один из самых простых способов – просмотреть название всех книг и найти ту, что в правильном алфавитном порядке должна быть первой, а затем поставить ее первой по счету на полку. После этого найти книгу, которая должна быть второй, и поставить ее после первой книги на ту полку. Так же третью, четвертую, и наконец \(n\)-ую книгу. Закончив раскладывать все книги, мы получим правильный ряд, расставленный в алфавитном порядке. В итоге получится, что количество действий, сделанных при расстановке, для очень большого количества книг будет примерно пропорционально квадрату количества книг. Именно это свойство помогает нам воспользоваться теоремой Пифагора и известными примитивными тройками:\[\text{Время для } 50 \text{ книг}= \text{Время для } 40 \text{ книг}+ \text{Время для } 30 \text{ книг}.\]Примечательно, что это будет работать с любыми объектами при их сортировки. Если рассмотреть общее количество операций и воспользоваться теоремой Пифагора, то обнаружиться что-то удивительное: количество операций для \(50\) объектов равно количеству операций для \(40\) и \(30\) объектов вместе взятых. Иначе говоря, \(70\) объектов, распределенные между двумя группами, могут быть отсортированы так же быстро, как \(50\) объектов в одной группе. Учитывая эту взаимосвязь, мы можем эффективнее разделить элементы на отдельные группы, а затем отсортировать эти подгруппы. Действительно, именно такой подход используется в быстрой сортировке – одном из лучших методов сортировки общего назначения.

Заключение

Теорема Пифагора – это не просто формула. Теорема Пифагора – сумма квадратов катетов, равная квадрату гипотенузе, изменившая мир. Простое равенство, берущее начало со времен пифагорейской математики, выведенное то ли вавилонскими учеными, то ли действительно Пифагором, смогло создать что-то большое и великое – человеческую цивилизацию. Древний Египет и Месопотамия, строительство домов и архитектура романских и готических соборов, современные социальные сети, радары и навигаторы – все, что связано с человеком, так же связано с теоремой Пифагора. В математике же теорема Пифагора занимает особенное место, и в ее кратком равенстве открывается простор для размышлений ученых всех времен, уверенных, что настоящая математика очаровательна, красива и увлекательна, как сама теорема Пифагора.

Данной статьей мы завершаем цикл "В чем прелесть математики". Мы надеемся, что наши публикации про изящество визуальных доказательств, вероятности и их связь с теоремой Байеса, разрезающих \(2000\) проводов Вовку и Азамата, а также таинственные бесконечности помогли вам взглянуть на математику под другим углом и стали очередным шагом в мире этой прелестной науки.

Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.

Редактор статьи: Дарина Мухамеджанова